
題目列表(包括答案和解析)
(1)證明![]() 對(duì)一切正整數(shù)n 成立;
對(duì)一切正整數(shù)n 成立;
(2)令![]() ,判斷
,判斷![]() 的大小,并說明理由。
的大小,并說明理由。
已知數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,且對(duì)一切正整數(shù)n都有
,且對(duì)一切正整數(shù)n都有![]() 。
。
(1)證明:![]() ;(2)求數(shù)列
;(2)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)設(shè) ,
,
求證:![]() 對(duì)一切
對(duì)一切![]() 都成立。
都成立。
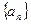 的前n項(xiàng)和為
的前n項(xiàng)和為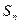 ,且對(duì)一切正整數(shù)n都有
,且對(duì)一切正整數(shù)n都有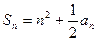 。
。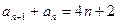 ;(2)求數(shù)列
;(2)求數(shù)列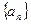 的通項(xiàng)公式;
的通項(xiàng)公式;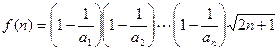 ,
,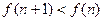 對(duì)一切
對(duì)一切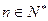 都成立。
都成立。
一、選擇題:每小題5分,共60分.
(1)D (2)A (3)D (4)A (5)B (6)C
(7)C (8)C (9)B (10)B (11)D (12)D
二、填空題:每小題4分,共16分.
(13)-2 (14)校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image180.gif) (15)
(15)校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image182.gif) (16)[-1,3]
(16)[-1,3]
三、解答題:共74分.
(17)(本小題12分)
解:校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image184.gif)
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image186.gif)
故該函數(shù)的最小正周期是校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image188.gif) ;最小值是-2;
;最小值是-2;
單增區(qū)間是[校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image190.gif) ],
],校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image192.gif)
(18)(本小題12分)
解:(I)校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image142.gif) 的所有可能值為0,1,2,3,4
的所有可能值為0,1,2,3,4
用AK表示“汽車通過第k個(gè)路口時(shí)不停(遇綠燈)”,
則P(AK)=校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image195.gif) 獨(dú)立.
獨(dú)立.
故校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image197.gif)
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image199.gif)
從而校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image201.gif) 有分布列:
有分布列:
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image202.gif) |
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image142.gif) 0 1 2
3 4
0 1 2
3 4
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image203.gif)
P 校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image205.gif)
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image207.gif)
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image209.gif)
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image211.gif)
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image213.gif)
校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image215.gif)
(II)校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image217.gif)
答:停車時(shí)最多已通過3個(gè)路口的概率為校招生全國統(tǒng)一考試(理工農(nóng)醫(yī)類)(重慶卷).files\image219.gif) .
.