
題目列表(包括答案和解析)
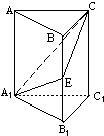
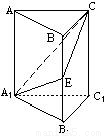
三棱柱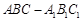 中,側棱與底面垂直,
中,側棱與底面垂直,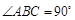 ,
,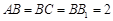 ,
,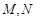 分別是
分別是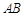 ,
, 的中點.
的中點.
(Ⅰ)求證: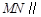 平面
平面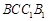 ;
;
(Ⅱ)求證: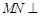 平面
平面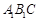 ;
;
(Ⅲ)求三棱錐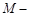
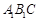 的體積.
的體積.
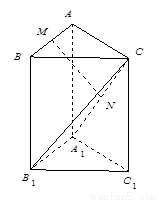
【解析】第一問利連結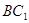 ,
,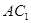 ,∵M,N是AB,
,∵M,N是AB, 的中點∴MN//
的中點∴MN//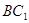 .
.
又∵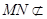 平面
平面 ,∴MN//平面
,∴MN//平面 .
. ----------4分
----------4分
⑵中年∵三棱柱ABC-A1B1C1中,側棱與底面垂直,∴四邊形 是正方形.∴
是正方形.∴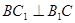 .∴
.∴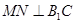 .連結
.連結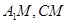 ,
,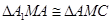 .
.
∴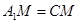 ,又N中
,又N中 的中點,∴
的中點,∴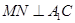 .
.
∵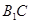 與
與 相交于點C,∴MN
相交于點C,∴MN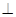 平面
平面 . --------------9分
. --------------9分
⑶中由⑵知MN是三棱錐M- 的高.在直角
的高.在直角 中,
中,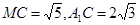 ,
,
∴MN=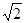 .又
.又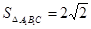 .
.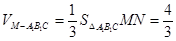 .得到結論。
.得到結論。
⑴連結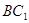 ,
,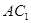 ,∵M,N是AB,
,∵M,N是AB, 的中點∴MN//
的中點∴MN//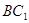 .
.
又∵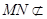 平面
平面 ,∴MN//平面
,∴MN//平面 .
. --------4分
--------4分
⑵∵三棱柱ABC-A1B1C1中,側棱與底面垂直,
∴四邊形 是正方形.∴
是正方形.∴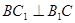 .
.
∴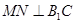 .連結
.連結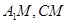 ,
,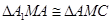 .
.
∴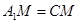 ,又N中
,又N中 的中點,∴
的中點,∴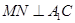 .
.
∵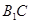 與
與 相交于點C,∴MN
相交于點C,∴MN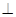 平面
平面 . --------------9分
. --------------9分
⑶由⑵知MN是三棱錐M- 的高.在直角
的高.在直角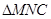 中,
中,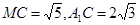 ,
,
∴MN=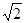 .又
.又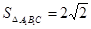 .
.
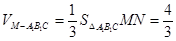
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
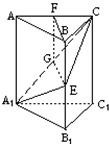
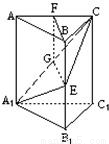
如圖,在正三棱柱ABC-A1B1C1中,底面ABC為正三角形,M、N、G分別是棱CC1、AB、BC的中點,且 .
.
(Ⅰ)求證:CN∥平面AMB1;
(Ⅱ)求證: B1M⊥平面AMG.

【解析】本試題主要是考查了立體幾何匯總線面的位置關系的運用。第一問中,要證CN∥平面AMB1;,只需要確定一條直線CN∥MP,既可以得到證明
第二問中,∵CC1⊥平面ABC,∴平面CC1 B1 B⊥平面ABC,得到線線垂直,B1M⊥AG,結合線面垂直的判定定理和性質定理,可以得證。
解:(Ⅰ)設AB1 的中點為P,連結NP、MP ………………1分


 ∵CM
∵CM  ,NP
,NP  ,∴CM
NP, …………2分
,∴CM
NP, …………2分
∴CNPM是平行四邊形,∴CN∥MP …………………………3分
∵CN 平面AMB1,MP奐 平面AMB1,∴CN∥平面AMB1…4分
(Ⅱ)∵CC1⊥平面ABC,∴平面CC1 B1 B⊥平面ABC,
∵AG⊥BC,∴AG⊥平面CC1 B1 B,∴B1M⊥AG………………6分
∵CC1⊥平面ABC,平面A1B1C1∥平面ABC,∴CC1⊥AC,CC1⊥B1 C,
設:AC=2a,則
 …………………………8分
…………………………8分
同理, …………………………………9分
…………………………………9分
∵ BB1∥CC1,∴BB1⊥平面ABC,∴BB1⊥AB,

 ………………………………10分
………………………………10分

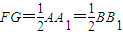 ,即
,即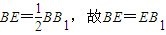 .
.如圖,在三棱柱 中,
中, 側面
側面 ,
, 為棱
為棱 上異于
上異于 的一點,
的一點, ,已知
,已知 ,求:
,求:
(Ⅰ)異面直線 與
與 的距離;
的距離;
(Ⅱ)二面角 的平面角的正切值.
的平面角的正切值.
【解析】第一問中,利用建立空間直角坐標系
解:(I)以B為原點, 、
、 分別為Y,Z軸建立空間直角坐標系.由于,
分別為Y,Z軸建立空間直角坐標系.由于,

在三棱柱 中有
中有
 ,
,
設


又 側面
側面 ,故
,故 . 因此
. 因此 是異面直線
是異面直線 的公垂線,則
的公垂線,則 ,故異面直線
,故異面直線 的距離為1.
的距離為1.
(II)由已知有 故二面角
故二面角 的平面角
的平面角 的大小為向量
的大小為向量 與
與 的夾角.
的夾角.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com