
題目列表(包括答案和解析)
(本小題滿分12分)如圖所示,已知圓![]()
|
足![]() 的軌跡為曲線E.
的軌跡為曲線E.
(1)求曲線E的方程;(II)若過定點F(0,2)
的直線交曲線E于不同的兩點G、H(點G在點F、H之間),
且滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
(本小題滿分12分)
如圖所示,已知S是正三角形ABC所在平面外的一點,且SA=SB=SC,SG為△SAB上的高,D、E、F分別是AC、BC、SC的中點,試判斷SG與平面DEF的位置關系,并給予證明.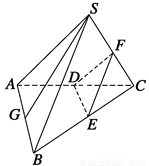
(本小題滿分12分)如圖所示,已知六棱錐 的底面是正六邊形,
的底面是正六邊形, 平面
平面 ,
, 是
是 的中點。
的中點。

(Ⅰ)求證:平面 //平面
//平面 ;
;
(Ⅱ)設 ,當二面角
,當二面角 的大小為
的大小為 時,求
時,求 的值。
的值。
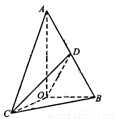
(本小題滿分12分)如圖所示,已知 中,
中,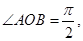 AB=2OB=4,D為AB的中點,若
AB=2OB=4,D為AB的中點,若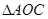 是
是 繞直線AO旋轉而成的,記二面角B—AO—C的大小為
繞直線AO旋轉而成的,記二面角B—AO—C的大小為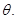 (I)若
(I)若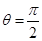 ,求證:平面
,求證:平面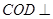 平面AOB;(II)若
平面AOB;(II)若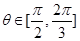 時,求二面角C—OD—B的余弦值的最小值。
時,求二面角C—OD—B的余弦值的最小值。
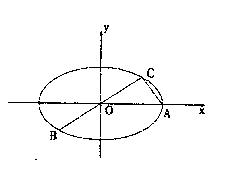
(本小題滿分12分)如圖所示,已知A、B、C是橢圓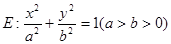 上三點,其中點A的坐標為
上三點,其中點A的坐標為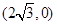 ,BC過橢圓的中心O,且
,BC過橢圓的中心O,且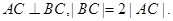
(Ⅰ)求點C的坐標及橢圓E的方程;
(Ⅱ)若橢圓E上存在兩點P, Q,使得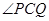 的平分線總垂直于z軸,試判斷向量
的平分線總垂直于z軸,試判斷向量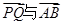 是否共線,并給出證明.
是否共線,并給出證明.
一:選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
B
B
B
B
D
B
D
C
C
A
二、填空題:
13、0
14、學.files/image212.gif)
15、 學.files/image214.gif)
16、①②
三、解答題:
學.files/image216.gif) 17、(Ⅰ)∵
17、(Ⅰ)∵
∴學.files/image218.gif) 的最大值為
的最大值為學.files/image220.gif) ,最小正周期是
,最小正周期是學.files/image222.gif) 。…………………6分
。…………………6分
注:得出表達式的簡化形式得4分,最大值、周期各得1分。
(Ⅱ)由(Ⅰ)知
學.files/image224.gif)
即學.files/image226.gif) 成立的
成立的學.files/image228.gif) 的取值集合是
的取值集合是學.files/image230.gif) ………10分
………10分
注:正確寫出正弦的單調增區(qū)間2分,答案正確2分。
18、解:(Ⅰ)學.files/image232.gif) ,
, 學.files/image234.gif)
學.files/image236.gif) ,
, 學.files/image238.gif)
隨機變量學.files/image240.gif) 的分布列為
的分布列為
學.files/image240.gif)
0
1
2
3
P
學.files/image243.gif)
學.files/image245.gif)
學.files/image247.gif)
學.files/image249.gif)
數(shù)學期望學.files/image251.gif) ………………………………………8分
………………………………………8分
注:每個概率算對得1分,分布列2分,期望2分。
(II)所求的概率學.files/image253.gif) …………12分
…………12分
注:知道概率加法公式得2分,結果正確得2分。
學.files/image255.gif) 19、(本題滿分12分)
19、(本題滿分12分)
證明:(1)在直三棱柱學.files/image143.gif) ,
,
∵底面三邊長學.files/image145.gif) ,
,學.files/image257.gif) ,
,學.files/image149.gif)
∴ 學.files/image260.gif) ,
--------------------------------1分
,
--------------------------------1分
又直三棱柱學.files/image262.gif) 中
中 學.files/image264.gif) ,
,
且學.files/image266.gif)
學.files/image268.gif)
∴學.files/image270.gif) ---------------------------------3分
---------------------------------3分
而學.files/image272.gif)
∴學.files/image274.gif) ;
---------------------------------4分
;
---------------------------------4分
(2)設學.files/image276.gif) 與
與學.files/image278.gif) 的交點為
的交點為學.files/image280.gif) ,連結
,連結學.files/image282.gif) ,---------------------5分
,---------------------5分
∵D是AB的中點,E是BC1的中點,
∴ 學.files/image284.gif) ,
----------------------------7分
,
----------------------------7分
∵ 學.files/image286.gif) ,
,學.files/image288.gif) ,
,
∴學.files/image290.gif) .
----------------------------8分
.
----------------------------8分
(3)過點C作CF⊥AB于F,連接C
由已知C1C垂直平面ABC,則∠C1FC為二面角學.files/image163.gif) 的平面角 ----------9分
的平面角 ----------9分
在Rt△ABC中,學.files/image293.gif) ,
,學.files/image147.gif) ,
,學.files/image296.gif) ,則
,則學.files/image298.gif) ----------10分
----------10分
又學.files/image300.gif)
∴ 學.files/image302.gif) ----------11分
----------11分
∴二面角學.files/image163.gif) 的正切值為
的正切值為學.files/image305.gif) ---------- 12分
---------- 12分
(另:可以建立空間直角坐標系用向量方法完成,酌情給分,過程略)
20、解(1)學.files/image307.gif)
∵學.files/image040.gif) 在
在學.files/image310.gif) 增函數(shù),(0,2)為減函數(shù)
增函數(shù),(0,2)為減函數(shù)
學.files/image312.gif) ………………………………………………2分
………………………………………………2分
(2)學.files/image314.gif) , …………………
4分
, …………………
4分
學.files/image316.gif) 5分
5分
學.files/image318.gif) ……………………7分
……………………7分
(3)學.files/image320.gif)
學.files/image322.gif)
學.files/image324.gif) ,
,學.files/image326.gif)
學.files/image328.gif)
學.files/image330.gif) ……………………………………………………………………12分
……………………………………………………………………12分
21、 解:(1)f(x)對任意學.files/image332.gif)
學.files/image334.gif) 2分
2分
令學.files/image336.gif)
學.files/image338.gif) 4分
4分
(2)解:數(shù)列{an}是等差數(shù)列 f(x)對任意x∈R都有學.files/image340.gif)
則令學.files/image342.gif) 5分
5分
學.files/image344.gif) ∴{an}是等差數(shù)列
8分
∴{an}是等差數(shù)列
8分
(3)解:由(2)有學.files/image346.gif) 9分
9分
學.files/image348.gif)
∴Tn≤Sn 該題也可用數(shù)學歸納法做。 12分
22、解:(1)∵學.files/image350.gif)
∴線段NP是AM的垂直平分線, 2分
∴學.files/image352.gif) 3分
3分
∵學.files/image354.gif)
∴點N的軌跡是以點C、A為焦點的橢圓; 4分
∴點N的軌跡E的方程是學.files/image356.gif) 5分
5分
(2)當直線的斜率不存在時,學.files/image358.gif) ,
,學.files/image360.gif) ,∴
,∴學.files/image362.gif) =
=學.files/image364.gif) ;
;學.files/image366.gif) 6分
6分
當直線的斜率存在時,設其方程為學.files/image368.gif) ,
,
學.files/image369.gif)
學.files/image356.gif)
學.files/image368.gif)
學.files/image373.gif) ,△
,△學.files/image375.gif) ,
,學.files/image377.gif) 7分
7分
設G(x1,y1),H(x2,y2)
學.files/image379.gif) ,
,學.files/image381.gif) ,∵
,∵學.files/image208.gif) ,∴
,∴學.files/image383.gif) 8分
8分
學.files/image385.gif) ,
,學.files/image387.gif) ,
,學.files/image389.gif) 9分
9分
學.files/image391.gif) ,
,學.files/image393.gif) ,
,學.files/image395.gif) ,
10分
,
10分
學.files/image397.gif) ,
,
∵點學.files/image202.gif) 在點
在點學.files/image206.gif) 、
、學.files/image204.gif) 之間 , ∴
之間 , ∴學.files/image362.gif) <1
11分
<1
11分
∴學.files/image362.gif) 的取值范圍是[
的取值范圍是[學.files/image401.gif) )。
)。
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com