15.(14分)如圖甲所示電路中,D為晶體二極管(正向電阻為零,反向電阻為無窮大),R1=R2=4Ω,R3=6Ω,當A、B間加上如圖乙所示的交變電壓時,求:
(1)在0~1×10-2s時間內,通過R1的電流;
(2)1s內電阻R3所消耗的電能。
16.(15分)1957年第一顆人造衛星上天,開辟了人類宇航的新時代。四十多年來,人類不僅發射了人造地球衛星,還向宇宙空間發射了多個空間探測器。空間探測器要飛向火星等其它行星,甚至飛出太陽系,首先要克服地球對它的引力的作用。理論研究表明,由于物體在地球附近受到地球對它的萬有引力的作用,具有引力勢能。設質量為m的物體在距地球無限遠處的引力勢能為零,則引力勢能表達式為EP=-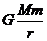 ,式中G是萬有引力常量,M是地球的質量,r是該物體距地心的距離。
,式中G是萬有引力常量,M是地球的質量,r是該物體距地心的距離。
(1)試證明空間探測器的最小發射速度與它繞地球勻速運行的最大環繞速度相等。
(2)現有一個質量為m的空間探測器繞地球做勻速圓周運動,運行周期為T,已知球半徑為R,地面附近的重力加速度為g。求該探測器做勻速圓周運動時的機械能(用m、g、R、T表示);
(3)在(2)的情形下,要使這個空間探測器從運行軌道上出發,脫離地球的引力作用,至少要對它作多少功?
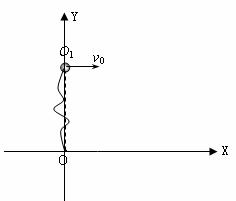 17.(15分)在光滑絕緣水平面上建立一水平直角坐標系,如圖所示,一質量為m、電量為q的帶正電小球,系于長為L的不可伸長的彈性輕繩的一端,繩的另一端固定在坐標原點O,現在水平面上加一電場強度大小為E=4mg/q,方向沿Y軸負方向的勻強電場。若把小球從O點的正上方距離O點
17.(15分)在光滑絕緣水平面上建立一水平直角坐標系,如圖所示,一質量為m、電量為q的帶正電小球,系于長為L的不可伸長的彈性輕繩的一端,繩的另一端固定在坐標原點O,現在水平面上加一電場強度大小為E=4mg/q,方向沿Y軸負方向的勻強電場。若把小球從O點的正上方距離O點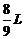 的O1點以速度
的O1點以速度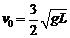 沿X軸正方向拋出。求:
沿X軸正方向拋出。求:
(1)輕繩即將伸直時,繩與豎直方向的夾角θ為多少?
(2)繩被拉直的瞬時,繩對小球所做的功?
(3)當小球再一次經過Y軸的瞬時,繩對小球的拉力為多大?
18.(16分)兩個正電荷Q1=Q和Q2=4Q分別置于固定在光滑絕緣水平面上的A、B兩點,A、B兩點相距L,且A、B兩點正好位于水平光滑絕緣半圓細管的兩個端點出口處,如圖所示。
(1)現將另一正點電荷置于A、B連線上靠近A處靜止釋放,它在AB連線上運動過程中速度最大的位置離A點的距離;
(2)若把該點電荷放于絕緣管內靠近A點處由靜止釋放,試求它在管內運動過程中速度最大時的位置P,即求PA和AB線的夾角θ(結果可用反三角函數表示)。
19.(16分) 如圖所示,一輕質彈簧將質量為m的小物塊連接在質量為M(M=3m)的光滑框架內。物塊位于框架中心位置時彈簧處于自由長度。現框架與物塊共同以速度v0沿光滑水平面向左勻速滑動。
(1)若框架與墻壁發生瞬間碰撞后速度為0且與墻不粘連,求框架剛要脫離墻壁時小物塊速度的大小和方向;
(2)在(1)情形下,框架脫離墻面后的運動過程中,彈簧彈性勢能的最大值Epm;

 D.物體溫度為
D.物體溫度為