
科目: 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).在以坐標原點為極點,
為參數(shù)).在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 相交于
相交于![]()
![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,在
,在![]() 軸上,是否存在點
軸上,是否存在點![]() ,使得無論非零實數(shù)
,使得無論非零實數(shù)![]() 怎樣變化,總有
怎樣變化,總有![]() 為直角?若存在,求出點
為直角?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數(shù)y=f(x)=![]() 。
。
(1)求y=f(x)的最大值;
(2)設實數(shù)a>0,求函數(shù)F(x)=af(x)在[a,2a]上的最小值。
查看答案和解析>>
科目: 來源: 題型:
【題目】某品牌汽車4S店,對該品牌旗下的A型、B型、C型汽車進行維修保養(yǎng),汽車4S店記錄了100輛該品牌三種類型汽車的維修情況,整理得下表:
車型 | A型 | B型 | C型 |
頻數(shù) | 20 | 40 | 40 |
假設該店采用分層抽樣的方法從上述維修的100輛該品牌三種類型汽車中隨機取10輛進行問卷回訪.
(1)求A型、B型、C型各車型汽車抽取的數(shù)目;
(2)維修結(jié)束后這100輛汽車的司機采用“100分制”打分的方式表示對4S店的滿意度,按照大于等于80為優(yōu)秀,小于80為合格,得到如下列聯(lián)表:
優(yōu)秀 | 合格 | 合計 | |
男司機 | 10 | 38 | 48 |
女司機 | 25 | 27 | 52 |
合計 | 35 | 65 | 100 |
問能否在犯錯誤概率不超過0.01的前提下認為司機對4S店滿意度與性別有關系?請說明原因.
(參考公式: )
)
附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 來源: 題型:
【題目】關于圓周率![]() ,數(shù)學發(fā)展史上出現(xiàn)過許多有創(chuàng)意的求法,如著名的普豐實驗和查理斯實驗.受其啟發(fā),我們也可以通過設計下面的實驗來估計
,數(shù)學發(fā)展史上出現(xiàn)過許多有創(chuàng)意的求法,如著名的普豐實驗和查理斯實驗.受其啟發(fā),我們也可以通過設計下面的實驗來估計![]() 的值:先請120名同學每人隨機寫下一個x,y都小于1的正實數(shù)對
的值:先請120名同學每人隨機寫下一個x,y都小于1的正實數(shù)對![]() ,再統(tǒng)計其中x,y能與1構(gòu)成鈍角三角形三邊的數(shù)對
,再統(tǒng)計其中x,y能與1構(gòu)成鈍角三角形三邊的數(shù)對![]() 的個數(shù)m,最后根據(jù)統(tǒng)計個數(shù)m估計
的個數(shù)m,最后根據(jù)統(tǒng)計個數(shù)m估計![]() 的值.如果統(tǒng)計結(jié)果是
的值.如果統(tǒng)計結(jié)果是![]() ,那么可以估計
,那么可以估計![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 為實數(shù),
為實數(shù),![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)是否存在實數(shù)![]() ,使得對任意給定的
,使得對任意給定的![]() ,在區(qū)間
,在區(qū)間![]() 上總存在三個不同的
上總存在三個不同的![]() ,使得
,使得![]() 成立?若存在,求出實數(shù)
成立?若存在,求出實數(shù)![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】2019年電商“雙十一”大戰(zhàn)即將開始.某電商為了盡快占領市場,搶占今年“雙十一”的先機,對成都地區(qū)年齡在15到75歲的人群“是否網(wǎng)上購物”的情況進行了調(diào)查,隨機抽取了100人,其年齡頻率分布表和使用網(wǎng)上購物的人數(shù)如下所示:(年齡單位:歲)
年齡段 |
|
|
|
|
|
|
頻率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
購物人數(shù) | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45歲為分界點,根據(jù)以上統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表,并判斷能否在犯錯誤的概率不超過0.001的前提下認為“網(wǎng)上購物”與年齡有關?
列聯(lián)表,并判斷能否在犯錯誤的概率不超過0.001的前提下認為“網(wǎng)上購物”與年齡有關?
年齡低于45歲 | 年齡不低于45歲 | 總計 | |
使用網(wǎng)上購物 | |||
不使用網(wǎng)上購物 | |||
總計 |
(2)若從年齡在![]() ,
,![]() 的樣本中各隨機選取2人進行座談,記選中的4人中“使用網(wǎng)上購物”的人數(shù)為
的樣本中各隨機選取2人進行座談,記選中的4人中“使用網(wǎng)上購物”的人數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
參考數(shù)據(jù):
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
參考公式: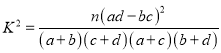
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖①,是由矩形![]() ,
,![]() 和
和![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() ,
,![]() ,將其沿
,將其沿![]() 折起使得
折起使得![]() 重合,連接
重合,連接![]() 如圖②.
如圖②.
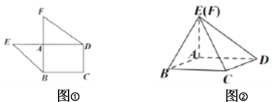
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() 中點,求直線
中點,求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數(shù)![]() 有極值,且導函數(shù)
有極值,且導函數(shù)![]() 的極值點是
的極值點是![]() 的零點,給出命題:①
的零點,給出命題:①![]() ;②若
;②若![]() ,則存在
,則存在![]() ,使得
,使得![]() ;③
;③![]() 與
與![]() 所有極值之和一定小于0;④若
所有極值之和一定小于0;④若![]() ,且
,且![]() 是曲線
是曲線![]() 的一條切線,則
的一條切線,則![]() 的取值范圍是
的取值范圍是![]() .則以上命題正確序號是_____________.
.則以上命題正確序號是_____________.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com