
科目: 來源: 題型:
【題目】已知![]() ,
, ![]() 滿足約束條件
滿足約束條件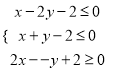 ,若
,若![]() 取得最大值的最優解不唯一,則實數
取得最大值的最優解不唯一,則實數![]() 的值為__________.
的值為__________.
【答案】![]() 或
或![]()
【解析】由題可知若![]() 取得最大值的最優解不唯一則
取得最大值的最優解不唯一則![]() 必平行于可行域的某一邊界,如圖:
必平行于可行域的某一邊界,如圖: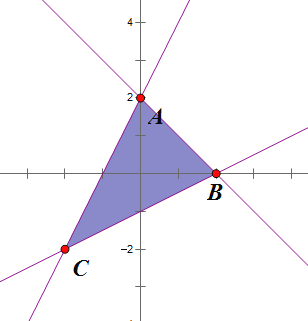 要Z最大則直線與y軸的截距最大即可,當a<0時,則平行AC直線即可故a=-2,當a>0時,則直線平行AB即可,故a=1
要Z最大則直線與y軸的截距最大即可,當a<0時,則平行AC直線即可故a=-2,當a>0時,則直線平行AB即可,故a=1
點睛:線性規劃為常考題型,解決此題務必要理解最優解個數為無數個時的條件是什么,然后根據幾何關系求解即可
【題型】填空題
【結束】
16
【題目】《數書九章》三斜求積術:“以小斜冪,并大斜冪,減中斜冪,余半之,自乘于上;以小斜冪乘大斜冪,減上,余四約一,為實,一為從隅,開平方得積”.秦九韶把三角形的三條邊分別稱為小斜、中斜和大斜,“術”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別表示三角形的面積,大斜,中斜,小斜;
分別表示三角形的面積,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分別為對應的大斜,中斜,小斜上的高;則
分別為對應的大斜,中斜,小斜上的高;則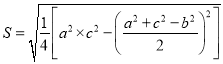
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根據上述公式,可以推出該三角形外接圓的半徑為__________.
,根據上述公式,可以推出該三角形外接圓的半徑為__________.
查看答案和解析>>
科目: 來源: 題型:
【題目】下列說法正確的是( )
A.設m為實數,若方程![]() 表示雙曲線,則m>2.
表示雙曲線,則m>2.
B.“p∧q為真命題”是“p∨q為真命題”的充分不必要條件
C.命題“x∈R,使得x2+2x+3<0”的否定是:“x∈R,x2+2x+3>0”
D.命題“若x0為y=f(x)的極值點,則f’(x)=0”的逆命題是真命題
查看答案和解析>>
科目: 來源: 題型:
【題目】定義:對于任意![]() ,滿足條件
,滿足條件![]() 且
且![]() (M是與n無關的常數)的無窮數列
(M是與n無關的常數)的無窮數列![]() 稱為M數列.
稱為M數列.
(1)若等差數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,判斷數列
,判斷數列![]() 是否是M數列,并說明理由;
是否是M數列,并說明理由;
(2)若各項為正數的等比數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,證明:數列
,證明:數列![]() 是M數列,并指出M的取值范圍;
是M數列,并指出M的取值范圍;
(3)設數列![]() ,問數列
,問數列![]() 是否是M數列?請說明理由.
是否是M數列?請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知動點P到直線![]() 的距離與到點
的距離與到點![]() 的距離之比為
的距離之比為![]() .
.
(1)求動點P的軌跡![]() ;
;
(2)直線![]() 與曲線
與曲線![]() 交于不同的兩點A,B(A,B在
交于不同的兩點A,B(A,B在![]() 軸的上方)
軸的上方)![]() :
:
①當A為橢圓與![]() 軸的正半軸的交點時,求直線
軸的正半軸的交點時,求直線![]() 的方程;
的方程;
②對于動直線![]() ,是否存在一個定點,無論
,是否存在一個定點,無論![]() 如何變化,直線
如何變化,直線![]() 總經過此定點?若存在,求出該定點的坐標;若不存在,請說明理由.
總經過此定點?若存在,求出該定點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】某公司要在一條筆直的道路邊安裝路燈,要求燈柱AB與底面垂直,燈桿BC與燈柱AB所在的平面與道路走向垂直,路燈C采用錐形燈罩,射出的管線與平面ABC部分截面如圖中陰影所示,![]() 路寬AD=24米,設
路寬AD=24米,設![]()

(1)求燈柱AB的高h(用![]() 表示);
表示);
(2)此公司應該如何設置![]() 的值才能使制作路燈燈柱AB和燈桿BC所用材料的總長度最小?最小值為多少?
的值才能使制作路燈燈柱AB和燈桿BC所用材料的總長度最小?最小值為多少?
查看答案和解析>>
科目: 來源: 題型:
【題目】已知等差數列![]() 的前
的前![]() 項和為
項和為![]() ,等比數列
,等比數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]()
(1)設![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)在(1)的條件下,且![]() ,求滿足
,求滿足![]() 的所有正整數
的所有正整數![]() ;
;
(3)若存在正整數![]() ,且
,且![]() ,試比較
,試比較![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知![]() 是關于的方程組
是關于的方程組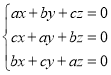 的解.
的解.
(1)求證: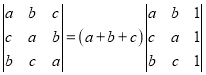 ;
;
(2)設![]() 分別為
分別為![]() 三邊長,試判斷
三邊長,試判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)設![]() 為不全相等的實數,試判斷
為不全相等的實數,試判斷![]() 是“
是“![]() ”的 條件,并證明.①充分非必要;②必要非充分;③充分且必要;④非充分非必要.
”的 條件,并證明.①充分非必要;②必要非充分;③充分且必要;④非充分非必要.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知拋物線![]() 的焦點為F,過焦點F的直線
的焦點為F,過焦點F的直線![]() 交拋物線于A,B兩點,設AB的中點為M,A,B,M在準線上的射影分別為C,D,N.
交拋物線于A,B兩點,設AB的中點為M,A,B,M在準線上的射影分別為C,D,N.
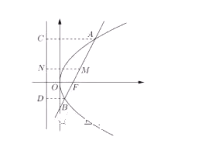
(1)求直線FN與直線AB的夾角![]() 的大小;
的大小;
(2)求證:點B,O,C三點共線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com