精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

【題目】對于函數，下列個結論正確的是__________（把你認為正確的答案全部寫上）．

（1）任取，都有；

（2）函數在上單調遞增；

（3），對一切恒成立；

（4）函數有個零點；

（5）若關于的方程有且只有兩個不同的實根，，則.

【題目】甲、乙兩位同學玩游戲，對于給定的實數，按下列方法操作一次產生一個新的實數：由甲、乙同時各擲一枚均勻的硬幣，如果出現兩個正面朝上或兩個反面朝上，則把乘以2后再減去12,；如果出現一個正面朝上，一個反面朝上，則把除以2后再加上12，這樣就得到一個新的實數，對實數仍按上述方法進行一次操作，又得到一個新的實數，當時，甲獲勝，否則乙獲勝，若甲獲勝的概率為，則的取值范圍是________

【題目】設曲線上一點到焦點的距離為3．

（1）求曲線C方程；

（2）設P，Q為曲線C上不同于原點O的任意兩點，且滿足以線段PQ為直徑的圓過原點O，試問直線PQ是否恒過定點？若恒過定點，求出定點坐標；若不恒過定點，說明理由．

【題目】2017年3月鄭州市被國務院確定為全國46個生活垃圾分類處理試點城市之一，此后由鄭州市城市管理局起草公開征求意見，經專家論證，多次組織修改完善，數易其稿，最終形成《鄭州市城市生活垃圾分類管理辦法》（以下簡稱《辦法》）．《辦法》已于2019年9月26日被鄭州市人民政府第35次常務會議審議通過，并于2019年12月1日開始施行．《辦法》中將鄭州市生活垃圾分為廚余垃圾、可回收垃圾、有害垃圾和其他垃圾4類．為了獲悉高中學生對垃圾分類的了解情況，某中學設計了一份調查問卷，500名學生參加測試，從中隨機抽取了100名學生問卷，記錄他們的分數，將數據分成7組：，，…，，并整理得到如下頻率分布直方圖：

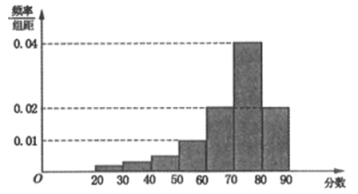
（1）從總體的500名學生中隨機抽取一人，估計其分數不低于60的概率；

（2）已知樣本中分數小于40的學生有5人，試估計總體中分數在區間內的學生人數，

（3）學校環保志愿者協會決定組織同學們利用課余時間分批參加“垃圾分類，我在實踐”活動，以增強學生的環保意識．首次活動從樣本中問卷成績低于40分的學生中隨機抽取2人參加，已知樣本中分數小于40的5名學生中，男生3人，女生2人，求抽取的2人中男女同學各1人的概率是多少？

A.B.C.D.

【題目】已知函數在區間上的最大值為，最小值為，記；

（1）求實數、的值；

（2）若不等式對任意恒成立，求實數的范圍；

（3）對于定義在上的函數，設，，用任意的將劃分為個小區間，其中，若存在一個常數，使得恒成立，則稱函數為上的有界變差函數；

①試證明函數是在上的有界變差函數，并求出的最小值；

②寫出是在上的有界變差函數的一個充分條件，使上述結論成為其特例；（不要求證明）

【題目】若數列的每一項都不等于零，且對于任意的，都有（為常數），則稱數列為“類等比數列”；已知數列滿足：，對于任意的，都有；

（1）求證：數列是“類等比數列”；

（2）若是單調遞減數列，求實數的取值范圍；

（3）若，求數列的前項之積取最大值時的值；

【題目】曲線上動點到定點與定直線的距離之比為常數；

（1）求曲線的軌跡方程；

（2）設圓心為的圓與曲線交于點與點，求的最小值，并求此時圓的方程；

【題目】設、、是集合，稱為有序三元組，如果集合、、滿足，且，則稱有序三元組為最小相交（其中表示集合中的元素個數），如集合，，就是最小相交有序三元組，則由集合的子集構成的最小相交有序三元組的個數是________

【題目】已知函數．

（1）若為單調函數，求a的取值范圍；

（2）若函數僅一個零點，求a的取值范圍．