精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

【題目】已知拋物線C：y2=2px過點P（1，1）.過點（0， ）作直線l與拋物線C交于不同的兩點M，N，過點M作x軸的垂線分別與直線OP，ON交于點A，B，其中O為原點.

（Ⅰ）求拋物線C的方程，并求其焦點坐標和準線方程；

（Ⅱ）求證：A為線段BM的中點.

甲、乙、丙三名射擊運動員射中目標的概率分別為，三人各射擊一次，擊中目標的次數記為.

（1）求的分布列及數學期望；

（2）在概率(=0，1，2，3)中, 若的值最大, 求實數的取值范圍.

【題目】已知函數,.

(1)若曲線在處的切線方程為,求的值；

（2）在(1)的條件下,求函數零點的個數；

（3）若不等式對任意都成立,求a的取值范圍.

【題目】已知橢圓的離心率，且經過點，，，，為橢圓的四個頂點（如圖），直線過右頂點且垂直于軸．

（1）求該橢圓的標準方程；

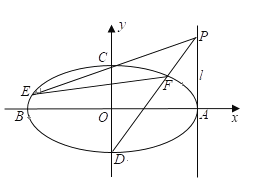
（2）為上一點（軸上方），直線，分別交橢圓于，兩點，若，求點的坐標．

【題目】如圖，射線和均為筆直的公路，扇形區域（含邊界）是一蔬菜種植園，其中、分別在射線和上.經測量得，扇形的圓心角（即）為、半徑為1千米.為了方便菜農經營，打算在扇形區域外修建一條公路，分別與射線、交于、兩點，并要求與扇形弧相切于點.設（單位：弧度），假設所有公路的寬度均忽略不計.

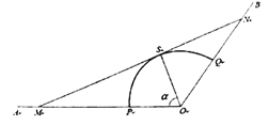
（1）試將公路的長度表示為的函數，并寫出的取值范圍；

（2）試確定的值，使得公路的長度最小，并求出其最小值.

【題目】對于，若數列滿足，則稱這個數列為“K數列”．

（Ⅰ）已知數列：1，m+1，m2是“K數列”，求實數的取值范圍；

（Ⅱ）是否存在首項為-1的等差數列為“K數列”，且其前n項和滿足

？若存在，求出的通項公式；若不存在，請說明理由；

（Ⅲ）已知各項均為正整數的等比數列是“K數列”，數列不是“K數列”，若，試判斷數列是否為“K數列”，并說明理由．

【題目】如圖，某園林單位準備綠化一塊直徑為BC的半圓形空地，△ABC外的地方種草，△ABC的內接正方形PQRS為一水池，其余的地方種花．若BC＝a，∠ABC＝，設△ABC的面積為S1,正方形的面積為S2．

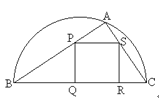
(1)用a，表示S1和S2；

(2)當a固定，變化時，求取最小值時的角．

【題目】已知函數的值域為A，.

(1)當的為偶函數時，求的值；

(2) 當時, 在A上是單調遞增函數，求的取值范圍；

(3)當時，（其中)，若，且函數的圖象關于點對稱，在處取 得最小值，試探討應該滿足的條件.

【題目】如圖所示：湖面上甲、乙、丙三艘船沿著同一條直線航行，某一時刻，甲船在最前面的點處，乙船在中間點處，丙船在最后面的點處，且.一架無人機在空中的點處對它們進行數據測量，在同一時刻測得， .（船只與無人機的大小及其它因素忽略不計）

（1）求此時無人機到甲、丙兩船的距離之比；

（2）若此時甲、乙兩船相距100米，求無人機到丙船的距離.（精確到1米）

【題目】已知函數，若在定義域內存在，使得成立，則稱為函數的局部對稱點.

（1）若、且，證明：函數必有局部對稱點；

（2）若函數在區間內有局部對稱點，求實數的取值范圍；

（3）若函數在上有局部對稱點，求實數的取值范圍.