
科目: 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
, ![]()
(1)當(dāng)![]() 時(shí),求不等式
時(shí),求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集為空集,求實(shí)數(shù)
的解集為空集,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來(lái)源: 題型:
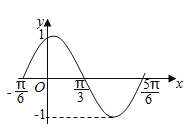
【題目】如圖是函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的圖象,為了得到這個(gè)函數(shù)的圖象,只需將
上的圖象,為了得到這個(gè)函數(shù)的圖象,只需將![]() 的圖象上的所有的點(diǎn)( )
的圖象上的所有的點(diǎn)( )
![]()
A.向左平移![]() 個(gè)長(zhǎng)度單位,再把所得各點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的
個(gè)長(zhǎng)度單位,再把所得各點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的![]() ,縱坐標(biāo)不變
,縱坐標(biāo)不變
B.向左平移![]() 個(gè)長(zhǎng)度單位,再把所得各點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的2倍,縱坐標(biāo)不變
個(gè)長(zhǎng)度單位,再把所得各點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的2倍,縱坐標(biāo)不變
C.向左平移![]() 個(gè)長(zhǎng)度單位,再把所得各點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的
個(gè)長(zhǎng)度單位,再把所得各點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的![]() ,縱坐標(biāo)不變
,縱坐標(biāo)不變
D.向左平移![]() 個(gè)長(zhǎng)度單位,再把所得各點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的2倍,縱坐標(biāo)不變
個(gè)長(zhǎng)度單位,再把所得各點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的2倍,縱坐標(biāo)不變
查看答案和解析>>
科目: 來(lái)源: 題型:
【題目】在直角坐標(biāo)系中,以原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸,以相同的長(zhǎng)度單位建立極坐標(biāo)系,已知直線
軸的正半軸為極軸,以相同的長(zhǎng)度單位建立極坐標(biāo)系,已知直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,曲線
,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,
,![]()
(l)設(shè)![]() 為參數(shù),若
為參數(shù),若![]() ,求直線
,求直線![]() 的參數(shù)方程;
的參數(shù)方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 設(shè)
設(shè)![]() ,且
,且![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目: 來(lái)源: 題型:
【題目】已知![]() 為圓
為圓![]() 上一點(diǎn),過(guò)點(diǎn)
上一點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 滿足
滿足![]()
(1)求動(dòng)點(diǎn)![]() 的軌跡方程;
的軌跡方程;
(2)設(shè)![]() 為直線
為直線![]() 上一點(diǎn),
上一點(diǎn),![]() 為坐標(biāo)原點(diǎn),且
為坐標(biāo)原點(diǎn),且![]() ,求
,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目: 來(lái)源: 題型:
【題目】如圖1,四棱錐![]() 的底面
的底面![]() 是正方形,
是正方形,![]() 垂直于底面
垂直于底面![]() ,已知四棱錐的正視圖,如圖2所示.
,已知四棱錐的正視圖,如圖2所示.
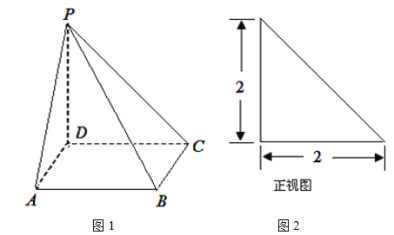
(I)若M是![]() 的中點(diǎn),證明:
的中點(diǎn),證明:![]() 平面
平面![]() ;
;
(II)求棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目: 來(lái)源: 題型:
【題目】唐三彩,中國(guó)古代陶瓷燒制工藝的珍品,它吸取了中國(guó)國(guó)畫(huà)、雕塑等工藝美術(shù)的特點(diǎn),在中國(guó)文化中占有重要的歷史地位,在中國(guó)的陶瓷史上留下了濃墨重彩的一筆.唐三彩的生產(chǎn)至今已有![]() 多年的歷史,對(duì)唐三彩的復(fù)制和仿制工藝,至今也有百余年的歷史.某陶瓷廠在生產(chǎn)過(guò)程中,對(duì)仿制的
多年的歷史,對(duì)唐三彩的復(fù)制和仿制工藝,至今也有百余年的歷史.某陶瓷廠在生產(chǎn)過(guò)程中,對(duì)仿制的![]() 件工藝品測(cè)得重量(單位:
件工藝品測(cè)得重量(單位:![]() )數(shù)據(jù)如下表:
)數(shù)據(jù)如下表:
分組 | 頻數(shù) | 頻率 |
|
|
|
|
| |
|
| |
|
|
|
|
| |
|
| |
合計(jì) |
|
(1)求出頻率分布表中實(shí)數(shù)![]() ,
,![]() 的值;
的值;
(2)若從仿制的![]() 件工藝品重量范圍在
件工藝品重量范圍在![]() 的工藝品中隨機(jī)抽選
的工藝品中隨機(jī)抽選![]() 件,求被抽選
件,求被抽選![]() 件工藝品重量均在范圍
件工藝品重量均在范圍![]() 中的概率.
中的概率.
查看答案和解析>>
科目: 來(lái)源: 題型:
【題目】“割圓術(shù)”是劉徽最突出的數(shù)學(xué)成就之一,他在《九章算術(shù)注》中提出割圓術(shù),并作為計(jì)算圓的周長(zhǎng),面積已經(jīng)圓周率的基礎(chǔ),劉徽把圓內(nèi)接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個(gè)近似數(shù)值,這個(gè)結(jié)果是當(dāng)時(shí)世界上圓周率計(jì)算的最精確數(shù)據(jù).如圖,當(dāng)分割到圓內(nèi)接正六邊形時(shí),某同學(xué)利用計(jì)算機(jī)隨機(jī)模擬法向圓內(nèi)隨機(jī)投擲點(diǎn),計(jì)算得出該點(diǎn)落在正六邊形內(nèi)的頻率為0.8269,那么通過(guò)該實(shí)驗(yàn)計(jì)算出來(lái)的圓周率近似值為(參考數(shù)據(jù):![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目: 來(lái)源: 題型:
【題目】已知二次函數(shù)![]() 的定義域
的定義域![]() 恰是不等式
恰是不等式![]() 的解集,其值域?yàn)?/span>
的解集,其值域?yàn)?/span>![]() ,函數(shù)
,函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,值域?yàn)?/span>
,值域?yàn)?/span>![]() .
.
(1)求![]() 定義域
定義域![]() 和值域
和值域![]() ;
;
(2)試用單調(diào)性的定義法解決問(wèn)題:若存在實(shí)數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,![]() 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù)![]() 的取值范圍并用
的取值范圍并用![]() 表示
表示![]() ;
;
(3)是否存在實(shí)數(shù)![]() ,使
,使![]() 成立?若存在,求實(shí)數(shù)
成立?若存在,求實(shí)數(shù)![]() 的取值范圍,若不存在,說(shuō)明理由.
的取值范圍,若不存在,說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com