【題目】已知
，
，且
，求
.
【答案】
【解析】試題分析：
首先求得cos(α－β)＝
，cosα＝
，sin(α－β)＝
.sinα＝
，由β＝α－(α－β)，得cosβ＝
，∴β＝
.
試題解析：
方法一 由0＜β＜α＜
，得0＜α－β＜.
又∵cos(α－β)＝，cosα＝，
∴sin(α－β)＝
＝
＝.
sinα＝
＝
＝，
由β＝α－(α－β)，得cosβ＝cos[α－(α－β)]
＝cosαcos(α－β)＋sinαsin(α－β)
＝×＋×＝，∴β＝.
方法二 由0＜β＜α＜，得0＜α－β＜.
又∵cos(α－β)＝，cosα＝
∴sin(α－β)＝＝＝.
sinα＝＝＝，
由β＝α－(α－β)，得sinβ＝sin[α－(α－β)]
＝sinαcos(α－β)－cosαsin(α－β)
＝×－×＝
，
∴
.
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
（
， 
）為奇函數(shù)，且相鄰兩對稱軸間的距離為
.
（1）當
時，求
的單調遞減區(qū)間；
（2）將函數(shù)
的圖象沿
軸方向向右平移
個單位長度，再把橫坐標縮短到原來的
（縱坐標不變），得到函數(shù)
的圖象.當
時，求函數(shù)
的值域.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在棱長為2的正方體
中， 
， 
， 
， 
分別是棱
， 
， 
， 
的中點，點
， 
分別在棱
， 
上移動，且
.
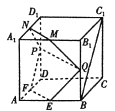
（1）當
時，證明：直線
平面
；
（2）是否存在
，使面
與面
所成的二面角為直二面角？若存在，求出
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為研究男女同學空間想象能力的差異，孫老師從高一年級隨機選取了20名男生、20名女生，進行空間圖形識別測試，得到成績莖葉圖如下，假定成績大于等于80分的同學為“空間想象能力突出”，低于80分的同學為“空間想象能力正常”.
（1）完成下面
列聯(lián)表，并判斷是否有
的把握認為“空間想象能力突出”與性別有關；
空間想象能力突出 | 空間想象能力正常 | 合計 | |
男生 | |||
女生 | |||
合計 |
（2）從“空間想象能力突出”的同學中隨機選取男生2名、女生2名，記其中成績超過90分的人數(shù)為
，求隨機變量
的分布列和數(shù)學期望.
下面公式及臨界值表僅供參考： 
| 0.100 | 0.050 | 0.010 | |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為了普及環(huán)保知識，增強環(huán)保意識，某校從理科甲班抽取60人，從文科乙班抽取50人參加環(huán)保知識測試．
優(yōu)秀人數(shù) | 非優(yōu)秀人數(shù) | 總計 | |
甲班 | |||
乙班 | 30 | ||
總計 | 60 |
（Ⅰ）根據(jù)題目完成
列聯(lián)表，并據(jù)此判斷是否有
的把握認為環(huán)保知識成績優(yōu)秀與學生的文理分類有關．
（Ⅱ）現(xiàn)已知
， 
， 
三人獲得優(yōu)秀的概率分別為
， 
， 
，設隨機變量
表示
， 
， 
三人中獲得優(yōu)秀的人數(shù)，求
的分布列及期望
．
附： 
， 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】山西某公司有一批專業(yè)技術人員，對他們進行年齡狀況和接受教育程度（本科學歷）的調查，其結果（人數(shù)分布）如表：
學歷 | 35歲以下 | 35 | 50歲以上 |
本科 | 80 | 30 | 20 |
研究生 |
| 20 |
|
（Ⅰ）用分層抽樣的方法在
歲年齡段的專業(yè)技術人員中抽取一個容量為10的樣本，將該樣本看成一個總體，從中任取3人，求至少有1人的學歷為研究生的概率；
（Ⅱ）在這個公司的專業(yè)技術人員中按年齡狀況用分層抽樣的方法抽取
個人，其中35歲以下48人，50歲以上10人，再從這個人中隨機抽取出1人，此人的年齡為50歲以上的概率為
，求
、
的值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
， 
（
為常數(shù)）.
（1）函數(shù)
的圖象在點
處的切線與函數(shù)
的圖象相切，求實數(shù)
的值；
（2）若函數(shù)
在定義域上存在單調減區(qū)間，求實數(shù)
的取值范圍；
（3）若
， 
，且
，都有
成立，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，D，E分別為△ABC邊AB，AC的中點，直線DE交△ABC的外接圓于F，G兩點，若CF∥AB，證明： 
（1）CD=BC；
（2）△BCD∽△GBD．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
