【題目】已知函數(shù)
，若
是函數(shù)
的零點，
是函數(shù)
的零點.
（1）比較與的大小；
（2）證明：
.
【答案】（1）
，見解析（2）見解析
【解析】
方法一：利用
，利用
對不等式進行放縮，可得
，
進而利用
單調(diào)遞增，且
和
，即可比較
與
的大小
方法二：設(shè)
，令函數(shù)
，從而判斷出函數(shù)的單調(diào)性，即可利用函數(shù)的單調(diào)性即可比較與的大小
(2) 令函數(shù)
，則
，要證
，即證
，只要證：
，最后通過證明函數(shù)
在區(qū)間
上的單調(diào)性進行證明即可.
（1）解:
方法一：
因為
，所以
，所以.
因為，且單調(diào)遞增，所以
方法二：設(shè)，
令函數(shù)
則
，則
則函數(shù)
在區(qū)間
上單調(diào)遞增，在區(qū)間
上單調(diào)遞減，
所以
所以
因為，且單調(diào)遞增，所以
（2）證明：令函數(shù)，
則.
要證，即證
只要證：，
只要證：函數(shù)在區(qū)間上單調(diào)遞減.
由題意得
因為
所以
所以
因為
單調(diào)遞增，所以在區(qū)間上，
所以
在區(qū)間上單調(diào)遞減.
所以原命題得證.
第1卷單元月考期中期末系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知線段
是過拋物線
的焦點F的一條弦，過點A（A在第一象限內(nèi)）作直線
垂直于拋物線的準(zhǔn)線，垂足為C，直線
與拋物線相切于點A，交x軸于點T，給出下列命題：
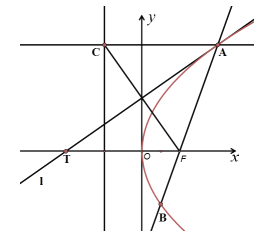
（1）
；
（2）
；
（3）
.
其中正確的命題個數(shù)為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在直角坐標(biāo)系
中，曲線
的參數(shù)方程為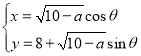
（
為參數(shù)，常數(shù)
）.以坐標(biāo)原點為極點，
軸的正半軸為極軸建立極坐標(biāo)系，已知直線
的極坐標(biāo)方程為
.
（1）寫出
及直線的直角坐標(biāo)方程，并指出是什么曲線；
（2）設(shè)
是曲線上的一個動點，求點到直線的距離的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】武漢某商場為促進市民消費，準(zhǔn)備每周隨機的從十個熱門品牌中抽取一個品牌送消費券，并且某個品牌被抽中后不再參與后面的抽獎，沒有抽中的品牌則繼續(xù)參加下周抽獎，假設(shè)每次抽取時各品牌被抽到的可能性相同，每次抽取也相互獨立.
（1）求某品牌到第三次才被抽到的概率；
（2）為了使更多品牌參加活動，商場做出調(diào)整，從第一周抽取后開始每周會有一個新的品牌補充進抽取隊伍，品牌A從第一周就開始參加抽獎，商場準(zhǔn)備開展半年（按26周計算）的抽獎活動，記品牌A參與抽獎的次數(shù)為X，試求X的數(shù)學(xué)期望（精確到0.01）.
參考數(shù)據(jù)：
，
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（1）當(dāng)
時，求函數(shù)
的極值；
（2）若對于任意實數(shù)
，當(dāng)
時，函數(shù)
的最大值為
，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
的內(nèi)角
，
，
的對邊分別為
，
，
，
.設(shè)
為線段
上一點，
，有下列條件：
①
；②
；③
.
請從以上三個條件中任選兩個，求
的大小和
的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
