D
[解析] 依題意得0<a<1，于是由f(1－
)>1得loga(1－)>logaa,0<1－<a，由此解得1<x<
，因此不等式f(1－)>1的解集是(1，)，選D.
B
[解析] 由題意知倉(cāng)儲(chǔ)x件需要的倉(cāng)儲(chǔ)費(fèi)為
元，所以平均費(fèi)用為y＝
＋
≥2
＝20，當(dāng)且僅當(dāng)x＝80等號(hào)成立．
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：
D
[解析] ⊙C1：(x＋a)2＋y2＝4的圓心C1(－a,0)，半徑r1＝2，⊙C2：x2＋(y－b)2＝1的圓心C2(0，b)，半徑r2＝1，
∵⊙C1與⊙C2外切，∴|C1C2|＝r1＋r2，
∴a2＋b2＝9，
∵(a＋b)2＝a2＋b2＋2ab≤2(a2＋b2)＝18，
∴a＋b≤3
，等號(hào)在a＝b＝
時(shí)成立．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
C
[解析] 依題意得
＋
＝(＋)[x＋(1－x)]＝13＋
＋
≥13＋2
＝25，當(dāng)且僅當(dāng)＝，即x＝
時(shí)取等號(hào)，選C.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
過(guò)平行六面體ABCD－A1B1C1D1任意兩條棱的中點(diǎn)作直線(xiàn)，其中與平面DBB1D1平行的直線(xiàn)共有( )
A．4條 B．6條
C．8條 D．12條
[答案] D
[解析] 如圖所示，設(shè)M、N、P、Q為所在邊的中點(diǎn)，
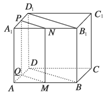
則過(guò)這四個(gè)點(diǎn)中的任意兩點(diǎn)的直線(xiàn)都與面DBB1D1平行，這種情形共有6條；同理，經(jīng)過(guò)BC、CD、B1C1、C1D1四條棱的中點(diǎn)，也有6條；故共有12條，故選D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
解析：依題意得f(x)的圖象關(guān)于直線(xiàn)x＝1對(duì)稱(chēng)，f(x＋1)＝－f(x－1)，f(x＋2)＝－f(x)，f(x＋4)＝－f(x＋2)＝f(x)，即函數(shù)f(x)是以4為周期的函數(shù)．由f(x)在[3,5]上是增函數(shù)與f(x)的圖象關(guān)于直線(xiàn)x＝1對(duì)稱(chēng)得，f(x)在[－3，－1]上是減函數(shù)．又函數(shù)f(x)是以4為周期的函數(shù)，因此f(x)在[1,3]上是減函數(shù)，f(x)在[1,3]上的最大值是f(1)，最小值是f(3)．
答案：A
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà)：027-86699610 舉報(bào)郵箱：58377363@163.com