
已知函數(shù)![]() ,
,![]() 且
且![]() .
.
(Ⅰ)求![]() 的定義域;
的定義域;
(Ⅱ)判斷![]() 的奇偶性并予以證明;
的奇偶性并予以證明;
(Ⅲ)當(dāng)![]() 時(shí),求使
時(shí),求使![]() 的
的![]() 的取值范圍.
的取值范圍.
(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 為奇函數(shù)(Ⅲ)
為奇函數(shù)(Ⅲ)![]()
(Ⅰ)![]() ,則
,則
![]() 解得
解得![]() .
.
故所求定義域?yàn)?img width=91 height=29 src="http://thumb.zyjl.cn/pic1/1899/sx/22/178422.gif" >.………………………………………………4分
(Ⅱ)由(Ⅰ)知![]() 的定義域?yàn)?img width=91 height=29 src="http://thumb.zyjl.cn/pic1/1899/sx/22/178422.gif" >,
的定義域?yàn)?img width=91 height=29 src="http://thumb.zyjl.cn/pic1/1899/sx/22/178422.gif" >,
且![]()
![]()
![]() ,
,
故![]() 為奇函數(shù). ………………………………………………………………9分
為奇函數(shù). ………………………………………………………………9分
(Ⅲ)因?yàn)楫?dāng)![]() 時(shí),
時(shí),![]() 在定義域
在定義域![]() 內(nèi)是增函數(shù),
內(nèi)是增函數(shù),
所以![]() .
.
解得![]() .
.
所以使![]() 的
的![]() 的取值范圍是
的取值范圍是![]() .
.


 導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2014屆河北棗強(qiáng)中學(xué)高二上學(xué)期期末考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù) ,且
,且 在
在 和
和 處取得極值.
處取得極值.
(1)求函數(shù) 的解析式.
的解析式.
(2)設(shè)函數(shù) ,是否存在實(shí)數(shù)
,是否存在實(shí)數(shù) ,使得曲線
,使得曲線 與
與 軸有兩個(gè)交點(diǎn),若存在,求出
軸有兩個(gè)交點(diǎn),若存在,求出 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014屆山西曲沃中學(xué)高二下學(xué)期第一次月考文科數(shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù)
 ,且
,且
(1)求 的值
的值
(2)判斷 在
在 上的單調(diào)性,并利用定義給出證明
上的單調(diào)性,并利用定義給出證明
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011學(xué)年江西省高三10月月考文科數(shù)學(xué)卷 題型:選擇題
已知函數(shù) ,若
,若 且
且 ,則下列不等式中正確的是( )
,則下列不等式中正確的是( )
A.  B.
B.
 C.
C.
 D.
D.
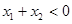
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011年江蘇省如皋市五校高二下學(xué)期期中考試文科數(shù)學(xué) 題型:選擇題
已知函數(shù) ,且
,且 ,
, .那么下列命題中真命題的序號(hào)是
.那么下列命題中真命題的序號(hào)是
① 的最大值為
的最大值為 ②
②  的最小值為
的最小值為
③ 在
在 上是減函數(shù)
④
上是減函數(shù)
④  在
在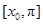 上是減函數(shù)
上是減函數(shù)
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2008年普通高等學(xué)校招生全國(guó)統(tǒng)一考試文科數(shù)學(xué)(北京卷) 題型:解答題
(本小題共13分)
已知函數(shù) ,且
,且 是奇函數(shù)。
是奇函數(shù)。
(Ⅰ)求 ,
, 的值;
的值;
(Ⅱ)求函數(shù) 的單調(diào)區(qū)間。
的單調(diào)區(qū)間。
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com