
【題目】已知直線![]() (
(![]() )與
)與![]() 軸交于
軸交于![]() 點,動圓
點,動圓![]() 與直線
與直線![]() 相切,并且與圓
相切,并且與圓![]() 相外切,
相外切,
(1)求動圓的圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若過原點且傾斜角為![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 兩點,問是否存在以
兩點,問是否存在以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
科目:高中數學 來源: 題型:
【題目】如圖,已知AB⊥平面ACD,DE⊥平面ACD,△ACD為等邊三角形,AD=DE=2AB,F為CD的中點. 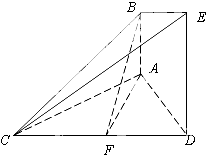
(1)求證:AF∥平面BCE;
(2)求證:平面BCE⊥平面CDE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市對創“市級示范性學校”的甲、乙兩所學校進行復查驗收,對辦學的社會滿意度一項評價隨機訪問了20為市民,這20位市民對這兩所學校的評分(評分越高表明市民的評價越好)的數據如下:
甲校:58,66,71,58,67,72,82,92,83,86,67,59,86,72,78,59,68,69,73,81;
乙校:90,80,73,65,67,69,81,85,82,88,89,86,86,78,98,95,96,91,76,69,.
檢查組將成績分成了四個等級:成績在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 為
為![]() 等.
等.

(1)請用莖葉圖表示上面的數據,并通過觀察莖葉圖,對兩所學校辦學的社會滿意度進行比較,寫出兩個統計結論;
(2)估計哪所學校的市民的評分等級為![]() 級或
級或![]() 級的概率大,說明理由.
級的概率大,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某大學自主招生的面試中,考生要從規定的6道科學題,4道人文題共10道題中,隨機抽取3道作答,每道題答對得10分,答錯或不答扣5分,已知甲、乙兩名考生參加面試,甲只能答對其中的6道科學題,乙答對每道題的概率都是![]() ,每個人答題正確與否互不影響.
,每個人答題正確與否互不影響.
(1)求考生甲得分![]() 的分布列和數學期望
的分布列和數學期望![]() ;
;
(2)求甲,乙兩人中至少有一人得分不少于15分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了了解該校學生對于某項運動的愛好是否與性別有關,通過隨機抽查110名學生,得到如下2×2的列聯表:
喜歡該項運動 | 不喜歡該項運動 | 總計 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
由公式![]() ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
參照附表,以下結論正確是( )
A. 有![]() 以上的把握認為“愛好該項運動與性別有關”
以上的把握認為“愛好該項運動與性別有關”
B. 有![]() 以上的把握認為“愛好該項運動與性別無關”
以上的把握認為“愛好該項運動與性別無關”
C. 有![]() 以上的把握認為“愛好該項運動與性別有關”
以上的把握認為“愛好該項運動與性別有關”
D. 有![]() 以上的把握認為“愛好該項運動與性別無關”
以上的把握認為“愛好該項運動與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線![]() 的焦點
的焦點![]() ,斜率為
,斜率為![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,且
兩點,且![]() .
.
(1)求該拋物線![]() 的方程;
的方程;
(2)已知拋物線上一點![]() ,過點
,過點![]() 作拋物線的兩條弦
作拋物線的兩條弦![]() 和
和![]() ,且
,且![]() ,判斷直線
,判斷直線![]() 是否過定點?并說明理由.
是否過定點?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
, ![]() 為參數),在以
為參數),在以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 是圓心在極軸上,且經過極點的圓.已知曲線
是圓心在極軸上,且經過極點的圓.已知曲線![]() 上的點
上的點 對應的參數
對應的參數![]() ,射線
,射線![]() 與曲線
與曲線![]() 交于點
交于點![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若點![]() ,
, ![]() 在曲線
在曲線![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com