
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() .
.
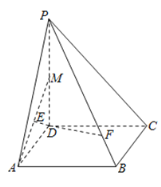
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 底面ABCD,且
底面ABCD,且![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)見解析(2)![]()
【解析】
(1)(法一)如圖,設(shè)![]() 中點(diǎn)為
中點(diǎn)為![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,則有
,則有![]() ,利用線面平行的判定定理,證得
,利用線面平行的判定定理,證得![]() 平面
平面![]() ,進(jìn)而證得
,進(jìn)而證得![]() 平面
平面![]() ,從而證得平面
,從而證得平面![]() 平面
平面![]() ,即可求得
,即可求得![]() 平面
平面![]() .
.
(法二)連接![]() 、
、![]() 、
、![]() ,則有
,則有![]() ,證得
,證得![]() ,利用線面平行的判定定理,即可證得
,利用線面平行的判定定理,即可證得![]() 平面
平面![]() .
.
(2)以![]() 為坐標(biāo)原點(diǎn)建立空間直角坐標(biāo)系
為坐標(biāo)原點(diǎn)建立空間直角坐標(biāo)系![]() ,求得平面
,求得平面![]() 和平面
和平面![]() 的一個法向量,利用向量的夾角公式,即可求解。
的一個法向量,利用向量的夾角公式,即可求解。
解:(1)證明:(法一)如圖,設(shè)![]() 中點(diǎn)為
中點(diǎn)為![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,則有
,則有![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() ,∴平面
,∴平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
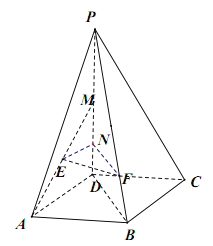
(法二)如圖,設(shè)![]() 中點(diǎn)為
中點(diǎn)為![]() ,
,![]() 為線段
為線段![]() 上一點(diǎn),且
上一點(diǎn),且![]() .
.
連接![]() 、
、![]() 、
、![]() ,則有
,則有![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,且
,且![]() ,
,
即![]() 為平行四邊形,∴
為平行四邊形,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
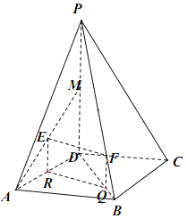
(2)∵平面![]() 底面
底面![]() ,且
,且![]() ,∴
,∴![]() 底面
底面![]() ,
,
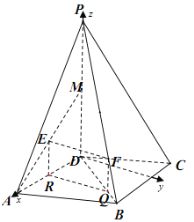
如圖,以![]() 為坐標(biāo)原點(diǎn)建立空間直角坐標(biāo)系
為坐標(biāo)原點(diǎn)建立空間直角坐標(biāo)系![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,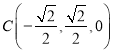 ,
,
∴![]() ,
,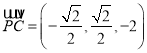 ,
,
設(shè)平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則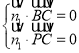 ,∴
,∴ ,
,
取![]() ,可得
,可得![]() ,
,
又易知平面![]() 的一個法向量
的一個法向量![]() ,
,
設(shè)平面![]() 與平面
與平面![]() 所成銳二面角為
所成銳二面角為![]() ,則
,則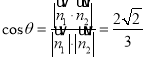 ,
,
∴平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.


 學(xué)練快車道快樂假期寒假作業(yè)系列答案
學(xué)練快車道快樂假期寒假作業(yè)系列答案 新思維寒假作業(yè)系列答案
新思維寒假作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若關(guān)于![]() 的方程
的方程![]() 有實(shí)數(shù)根,求實(shí)數(shù)
有實(shí)數(shù)根,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標(biāo)系中,曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() ,點(diǎn)
,點(diǎn)![]() 是曲線
是曲線![]() 上的動點(diǎn).點(diǎn)
上的動點(diǎn).點(diǎn)![]() 滿足
滿足![]() (
(![]() 為極點(diǎn)).設(shè)點(diǎn)
為極點(diǎn)).設(shè)點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .以極點(diǎn)
.以極點(diǎn)![]() 為原點(diǎn),極軸為
為原點(diǎn),極軸為![]() 軸的正半軸建立平面直角坐標(biāo)系
軸的正半軸建立平面直角坐標(biāo)系![]() ,已知直線
,已知直線![]() 的參數(shù)方程是
的參數(shù)方程是![]() ,(
,(![]() 為參數(shù)).
為參數(shù)).
(1)求曲線![]() 的直角坐標(biāo)方程與直線
的直角坐標(biāo)方程與直線![]() 的普通方程;
的普通方程;
(2)設(shè)直線![]() 交兩坐標(biāo)軸于
交兩坐標(biāo)軸于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高中志愿者部有男志愿者6人,女志愿者4人,這些人要參加元旦聯(lián)歡會的服務(wù)工作. 從這些人中隨機(jī)抽取4人負(fù)責(zé)舞臺服務(wù)工作,另外6人負(fù)責(zé)會場服務(wù)工作.
(Ⅰ)設(shè)![]() 為事件:“負(fù)責(zé)會場服務(wù)工作的志愿者中包含女志愿者
為事件:“負(fù)責(zé)會場服務(wù)工作的志愿者中包含女志愿者![]() 但不包含男志愿者
但不包含男志愿者![]() ”,求事件
”,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
(Ⅱ)設(shè)![]() 表示參加舞臺服務(wù)工作的女志愿者人數(shù),求隨機(jī)變量
表示參加舞臺服務(wù)工作的女志愿者人數(shù),求隨機(jī)變量![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象在
的圖象在![]() 軸右側(cè)的第一個最高點(diǎn)和第一個最低點(diǎn)的坐標(biāo)分別為
軸右側(cè)的第一個最高點(diǎn)和第一個最低點(diǎn)的坐標(biāo)分別為![]() 和
和![]() .若將函數(shù)
.若將函數(shù)![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度后得到的圖象關(guān)于原點(diǎn)對稱.
個單位長度后得到的圖象關(guān)于原點(diǎn)對稱.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)若函數(shù)![]() 的周期為
的周期為![]() ,當(dāng)
,當(dāng)![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實(shí)數(shù)
恰有兩個不同的解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】朱世杰是歷史上最偉大的數(shù)學(xué)家之一,他所著的![]() 四元玉鑒
四元玉鑒![]() 卷中“如像招數(shù)”五問有如下問題:“今有官司差夫一千八百六十四人筑堤
卷中“如像招數(shù)”五問有如下問題:“今有官司差夫一千八百六十四人筑堤![]() 只云初日差六十四人,次日轉(zhuǎn)多七人,每人日支米三升,共支米四百三石九斗二升,問筑堤幾日”
只云初日差六十四人,次日轉(zhuǎn)多七人,每人日支米三升,共支米四百三石九斗二升,問筑堤幾日”![]() 其大意為:“官府陸續(xù)派遣
其大意為:“官府陸續(xù)派遣![]() 人前往修筑堤壩,第一天派出
人前往修筑堤壩,第一天派出![]() 人,從第二天開始,每天派出的人數(shù)比前一天多
人,從第二天開始,每天派出的人數(shù)比前一天多![]() 人,修筑堤壩的每人每天分發(fā)大米
人,修筑堤壩的每人每天分發(fā)大米![]() 升,共發(fā)出大米
升,共發(fā)出大米![]() 升,問修筑堤壩多少天”
升,問修筑堤壩多少天”![]() 這個問題中,前
這個問題中,前![]() 天一共應(yīng)發(fā)大米____________升.
天一共應(yīng)發(fā)大米____________升.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)若函數(shù)![]() 有兩個極值點(diǎn)
有兩個極值點(diǎn)![]() 且
且![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,ABCD是一塊邊長為7米的正方形鐵皮,其中ATN是一半徑為6米的扇形,已經(jīng)被腐蝕不能使用,其余部分完好可利用.工人師傅想在未被腐蝕部分截下一個有邊落在BC與CD上的長方形鐵皮![]() ,其中P是弧TN上一點(diǎn).設(shè)
,其中P是弧TN上一點(diǎn).設(shè)![]() ,長方形
,長方形![]() 的面積為S平方米.
的面積為S平方米.
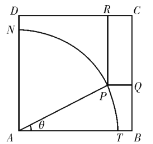
(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《算法統(tǒng)宗》是中國古代數(shù)學(xué)名著,由明代數(shù)學(xué)家程大位所著,該作完善了珠算口訣,確立了算盤用法,完成了由籌算到珠算的徹底轉(zhuǎn)變,該作中有題為“李白沽酒”“李白街上走,提壺去買酒。遇店加一倍,見花喝一斗,三遇店和花,喝光壺中酒。借問此壺中,原有多少酒?”,如圖為該問題的程序框圖,若輸出的![]() 值為0,則開始輸入的
值為0,則開始輸入的![]() 值為( )
值為( )
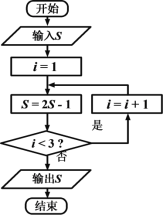
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com