分析:(1)由于本題中已知點A(λcosα,λsinα)(λ≠0),
B(,-),O為坐標原點,不等式
||≥2||有解即存在這樣的參數使得不等式成立,這是一個存在性問題,故通過向量的模的表達公式轉化為關于參數λ的不等式有解的問題,解出它的取值范圍;
(2)相比(1)本小題是一個恒成立問題,可將不等式進行化簡,利用三角函數的有界性轉化為關于參數λ的不等式;
解答:解:(1)
||≥2||有解,即
(λcosα-)2+(λsinα+)2≥4(2分)
等價于:
λ2+1+2λsin(α-)≥4,代入
α=得:λ
2≥3(4分)
即
λ∈(-∞,-]∪[,+∞)(6分)
(2)
||≥2||對任意的實數α恒成立,即
(λcosα-)2+(λsinα+)2≥4對任意的實數α恒成立,即
λ2+1+2λsin(α-)≥4對任意的實數α恒成立 (8分)
所以
或
(12分)
解得:λ≥3或λ≤-3.故所求實數λ的取值范圍是(-∞,-3]∪[3,+∞).(14分)
點評:本題是一個向量綜合題,本題考查了存在性問題與恒成立問題,解此類題關鍵是對存在問題與恒成立問題進行轉化,理解這類問題的邏輯關系是正確轉化的關鍵,此類題是高中數學的難點,也是容易互相混淆的題,熟練掌握向量模的坐標表示公式是本題轉化的知識保證,本題比較抽象,考查了推理判斷能力以及計算能力,轉化化歸的思想,思維有深度,是高中數學中較易出錯的難題



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案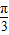 ),sin(α+
),sin(α+ )),點C(1,0).
)),點C(1,0).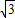 ,求α的值;
,求α的值;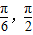 ),求
),求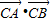 的取值范圍.
的取值范圍.