
(本小題滿分13分)已知函數
 .
.
(1)若 為
為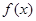 的極值點,求實數
的極值點,求實數 的值;
的值;
(2)若 在
在 上為增函數,求實數
上為增函數,求實數 的取值范圍;
的取值范圍;
(3)當 時,方程
時,方程 有實根,求實數
有實根,求實數 的最大值.
的最大值.
(1)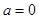 .(2)
.(2)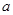 的取值范圍為
的取值范圍為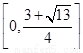 .(3)當
.(3)當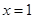 時,
時,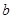 有最大值0.
有最大值0.
【解析】(1)根據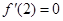 建立關于a的方程求出a的值.
建立關于a的方程求出a的值.
(2)本小題實質是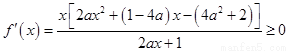 在區(qū)間
在區(qū)間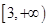 上恒成立,
上恒成立,
進一步轉化為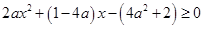 在區(qū)間
在區(qū)間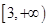 上恒成立,
上恒成立,
然后再討論a=0和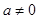 兩種情況研究.
兩種情況研究.
(2) 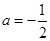 時,方程
時,方程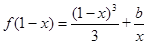 可化為,
可化為,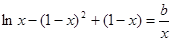 ,
,
問題轉化為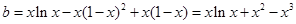 在
在 上有解,
上有解,
即求函數 的值域,然后再利用導數研究g(x)的單調區(qū)間極值最值,從而求出值域,問題得解.
的值域,然后再利用導數研究g(x)的單調區(qū)間極值最值,從而求出值域,問題得解.
解:(1)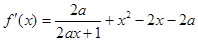
 .………1分
.………1分
因為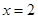 為
為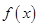 的極值點,所以
的極值點,所以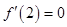 .………………………2分
.………………………2分
即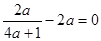 ,解得
,解得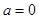 .…………………………………3分
.…………………………………3分
又當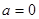 時,
時,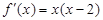 ,從而
,從而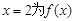 的極值點成立.…………4分
的極值點成立.…………4分
(2)因為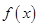 在區(qū)間
在區(qū)間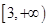 上為增函數,
上為增函數,
所以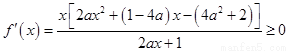 在區(qū)間
在區(qū)間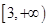 上恒成立.…5分
上恒成立.…5分
①當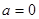 時,
時, 在
在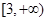 上恒成立,所以
上恒成立,所以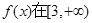 上為增函數,故
上為增函數,故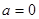
符合題意.…………………………6分
②當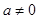 時,由函數
時,由函數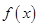 的定義域可知,必須有
的定義域可知,必須有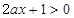 對
對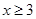 恒成立,故只能
恒成立,故只能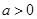 ,
,
所以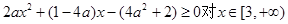 上恒成立.……………7分
上恒成立.……………7分
令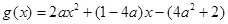 ,其對稱軸為
,其對稱軸為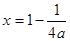 ,……………8分
,……………8分
因為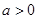 所以
所以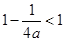 ,從而
,從而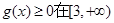 上恒成立,只要
上恒成立,只要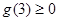 即可,
即可,
因為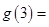
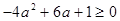 ,
,
解得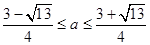 . u……………………………………9分
. u……………………………………9分
因為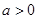 ,所以
,所以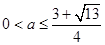 .
.
綜上所述,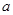 的取值范圍為
的取值范圍為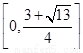 .…………………………………10分
.…………………………………10分
(3)若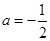 時,方程
時,方程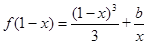 可化為,
可化為,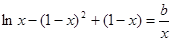 .
.
問題轉化為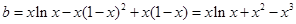 在
在 上有解,
上有解,
即求函數 的值域.……………………11分
的值域.……………………11分
以下給出兩種求函數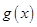 值域的方法:
值域的方法:
方法1:因為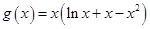 ,令
,令 ,
,
則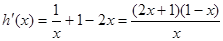 ,…………………………………12分
,…………………………………12分
所以當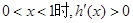 ,從而
,從而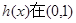 上為增函數,
上為增函數,
當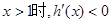 ,從而
,從而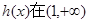 上為減函數,………………………13分
上為減函數,………………………13分
因此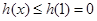 .
.
而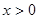 ,故
,故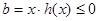 ,
,
因此當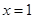 時,
時,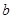 取得最大值0.…………………………………………14分
取得最大值0.…………………………………………14分
方法2:因為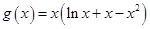 ,所以
,所以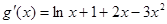 .
.
設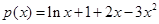 ,則
,則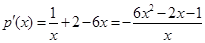 .
.
當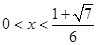 時,
時,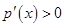 ,所以
,所以 在
在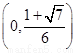 上單調遞增;
上單調遞增;
當 時,
時, ,所以
,所以 在
在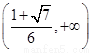 上單調遞減;
上單調遞減;
因為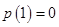 ,故必有
,故必有 ,又
,又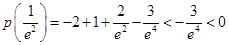 ,
,
因此必存在實數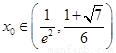 使得
使得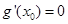 ,
,
 ,所以
,所以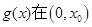 上單調遞減;
上單調遞減;
當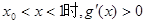 ,所以
,所以 上單調遞增;
上單調遞增;
當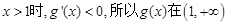 上單調遞減;
上單調遞減;
又因為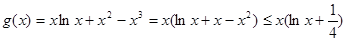 ,
,
當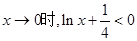 ,則
,則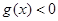 ,又
,又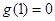 .
.
因此當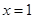 時,
時,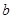 取得最大值0.……………………………14分
取得最大值0.……………………………14分


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源:2015屆江西省高一第二次月考數學試卷(解析版) 題型:解答題
(本小題滿分13分)已知函數
 .
.
(1)求函數 的最小正周期和最大值;
的最小正周期和最大值;
(2)在給出的直角坐標系中,畫出函數 在區(qū)間
在區(qū)間 上的圖象.
上的圖象.
(3)設0<x< ,且方程
,且方程 有兩個不同的實數根,求實數m的取值范圍.
有兩個不同的實數根,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三年級八月份月考試卷理科數學 題型:解答題
(本小題滿分13分)已知定義域為 的函數
的函數 是奇函數.
是奇函數.
(1)求 的值;(2)判斷函數
的值;(2)判斷函數 的單調性;
的單調性;
(3)若對任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范圍.
,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源:河南省09-10學年高二下學期期末數學試題(理科) 題型:解答題
(本小題滿分13分)如圖,正三棱柱 的所有棱長都為2,
的所有棱長都為2, 為
為 的中點。
的中點。
(Ⅰ)求證: ∥平面
∥平面 ;
;
(Ⅱ)求異面直線 與
與 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[來源:KS5
U.COM
查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省高三5月月考調理科數學 題型:解答題
(本小題滿分13分)
已知 為銳角,且
為銳角,且 ,函數
,函數 ,數列{
,數列{ }的首項
}的首項 .
.
(1) 求函數 的表達式;
的表達式;
(2)在 中,若
中,若 A=2
A=2 ,
, ,BC=2,求
,BC=2,求 的面積
的面積
(3) 求數列 的前
的前 項和
項和
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com