【題目】在平面直角坐標系
中，曲線
的參數(shù)方程為
(
為參數(shù)），以
為極點， 
軸的非負半軸為極軸的極坐標系中，直線
的極坐標方程為
.
（1）求曲線
的極坐標方程；
（2）設直線
與曲線
相交于
兩點，求
的值.
【答案】（1）曲線
的極坐標方程為： 
；（2）6.
【解析】試題分析：（1）先根據(jù)三角函數(shù)平方關系消參數(shù)得曲線
的普通方程，再根據(jù)
化為極坐標方程；（2）將直線l的極坐標方程代入曲線
的極坐標方程得
，再根據(jù)
求
的值．
試題解析：解:（1）將方程
消去參數(shù)
得
，
∴曲線
的普通方程為
，
將
代入上式可得
，
∴曲線
的極坐標方程為： 
． -
（2）設
兩點的極坐標方程分別為
,
由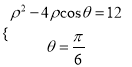
消去
得
，
根據(jù)題意可得
是方程
的兩根，
∴
，
∴
．
【題型】解答題
【結束】
23
【題目】選修4—5：不等式選講
已知函數(shù)
．
(1)當
時，求關于x的不等式
的解集；
(2)若關于x的不等式
有解，求a的取值范圍．
點睛新教材全能解讀系列答案
小學教材完全解讀系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線E：
的焦點為F，
是拋物線E上一點，且
．
1
求拋物線E的標準方程；
2設點B是拋物線E上異于點A的任意一點，直線AB與直線
交于點P，過點P作x軸的垂線交拋物線E于點M，設直線BM的方程為
，k，b均為實數(shù)，請用k的代數(shù)式表示b，并說明直線BM過定點．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】通過隨機詢問100名性別不同的大學生是否愛好踢毽子，得到如下的列聯(lián)表：
隨機變量
經(jīng)計算，統(tǒng)計量K2的觀測值k0≈4.762，參照附表，得到的正確結論是( )
A. 在犯錯誤的概率不超過5%的前提下，認為“愛好該項運動與性別有關”
B. 在犯錯誤的概率不超過5%的前提下，認為“愛好該項運動與性別無關”
C. 有97.5%以上的把握認為“愛好該項運動與性別有關”
D. 有97.5%以上的把握認為“愛好該項運動與性別無關”
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=xcos+a，a∈R.
（I）求曲線y=f（x）在點x=
處的切線的斜率；
（II）判斷方程f '（x）=0（f '（x）為f（x）的導數(shù)）在區(qū)間（0，1）內的根的個數(shù)，說明理由；
（III）若函數(shù)F（x）=xsinx+cosx+ax在區(qū)間（0，1）內有且只有一個極值點，求a的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
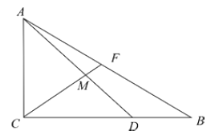
【題目】在三角形ABC中，
，
，
，D是線段BC上一點，且
，F為線段AB上一點．
（1）若
，求
的值；
（2）求
的取值范圍；
（3）若
為線段
的中點，直線
與
相交于點
，求
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
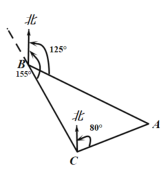
【題目】如圖，貨輪在海上B處，以50海里/時的速度沿方位角（從正北方向順時針轉到目標方向線的水平角）為155o的方向航行，為了確定船位，在B點處觀測到燈塔A的方位角為125o．半小時后，貨輪到達C點處，觀測到燈塔A的方位角為80o．求此時貨輪與燈塔之間的距離（答案保留最簡根號）．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知等差數(shù)列{an}的前n項的和記為Sn．如果a4＝－12，a8＝－4．
(1)求數(shù)列{an}的通項公式；
(2)求Sn的最小值及其相應的n的值；
(3)從數(shù)列{an}中依次取出a1，a2，a4，a8，…，
，…，構成一個新的數(shù)列{bn}，求{bn}的前n項和
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
