
已知數列{an}前n項和為Sn,且a2an=S2+Sn對一切正整數都成立.
(1)求a1,a2的值;
(2)設a1>0,數列 前n項和為Tn,當n為何值時,Tn最大?并求出最大值.
前n項和為Tn,當n為何值時,Tn最大?并求出最大值.
(1)a1=0,a2=0或a1=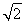 +1,a2=
+1,a2=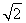 +2或a1=1-
+2或a1=1-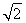 ,a2=2-
,a2=2-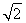 .(2)n=7時,Tn取得最大值,T7=7-
.(2)n=7時,Tn取得最大值,T7=7- lg2.
lg2.
【解析】(1)取n=1時,a2a1=S2+S1=2a1+a2,①
取n=2時,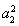 =2a1+2a2.②由②-①得,a2(a2-a1)=a2.③
=2a1+2a2.②由②-①得,a2(a2-a1)=a2.③
若a2=0,由①知a1=0;若a2≠0,由③知a2-a1=1.④
由①④解得a1= +1,a2=2+
+1,a2=2+ 或a1=1-
或a1=1-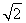 ,a2=2-
,a2=2- .
.
綜上所述,a1=0,a2=0或a1=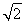 +1,a2=
+1,a2=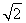 +2或a1=1-
+2或a1=1-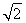 ,a2=2-
,a2=2-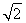 .
.
(2)當a1>0時,a1=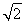 +1,a2=
+1,a2= +2.
+2.
n≥2時,有(2+ )an=S2+Sn,(2+
)an=S2+Sn,(2+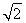 )an-1=S2+Sn-1,
)an-1=S2+Sn-1,
∴(1+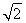 )an=(2+
)an=(2+ )an-1,即an=
)an-1,即an= an-1(n≥2),
an-1(n≥2),
∴an=a1( )n-1=(
)n-1=(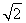 +1)(
+1)(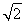 )n-1.令bn=
)n-1.令bn= =1-
=1-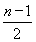 lg2,
lg2,
故{bn}是遞減的等差數列,從而b1>b2>…>b7=lg >lg1=0,
>lg1=0,
n≥8時,bn≤b8= lg
lg <
< lg1=0,故n=7時,Tn取得最大值,T7=7-
lg1=0,故n=7時,Tn取得最大值,T7=7- lg2
lg2


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第八章第3課時練習卷(解析版) 題型:填空題
如圖所示,b,c在平面α內,a∩c=B,b∩c=A,且a⊥b,a⊥c,b⊥c,若C∈a,D∈b,E在線段AB上(C、D、E均異于A、B),則△ACD的形狀是________.

查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第八章第1課時練習卷(解析版) 題型:解答題
如圖,四邊形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥=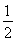 AD,BE∥=
AD,BE∥=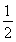 FA,G、H分別為FA、FD的中點.
FA,G、H分別為FA、FD的中點.
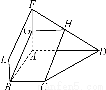
(1)證明:四邊形BCHG是平行四邊形.
(2)C、D、F、E四點是否共面?為什么?
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第6課時練習卷(解析版) 題型:解答題
已知數列{an}中,a1=2,n∈N*,an>0,數列{an}的前n項和為Sn,且滿足an+1=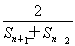 .
.
(1)求{Sn}的通項公式;
(2)設{bk}是{Sn}中的按從小到大順序組成的整數數列.
①求b3;
②存在N(N∈N*),當n≤N時,使得在{Sn}中,數列{bk}有且只有20項,求N的范圍.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第6課時練習卷(解析版) 題型:填空題
根據市場調查結果,預測某種家用商品從年初開始的n個月內累積的需求量Sn(萬件)近似地滿足關系式Sn=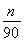 (21n-n2-5)(n=1,2,…,12),按此預測,在本年度內,需求量超過1.5萬件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此預測,在本年度內,需求量超過1.5萬件的月份是________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第5課時練習卷(解析版) 題型:解答題
已知等差數列{an}滿足:an+1>an(n∈N*),a1=1,該數列的前三項分別加上1,1,3后順次成為等比數列{bn}的前三項.
(1)分別求數列{an}、{bn}的通項公式;
(2)設Tn= (n∈N*),若Tn+
(n∈N*),若Tn+ <c(c∈Z)恒成立,求c的最小值.
<c(c∈Z)恒成立,求c的最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第4課時練習卷(解析版) 題型:解答題
已知數列{an}的前n項和為Sn,對一切正整數n,點Pn(n,Sn)都在函數f(x)=x2+2x的圖象上,且在點Pn(n,Sn)處的切線的斜率為kn.
(1)求數列{an}的通項公式;
(2)若bn=2knan,求數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第3課時練習卷(解析版) 題型:解答題
已知數列{an}的首項a1=2a+1(a是常數,且a≠-1),
an=2an-1+n2-4n+2(n≥2),數列{bn}的首項b1=a,
bn=an+n2(n≥2).
(1)證明:{bn}從第2項起是以2為公比的等比數列;
(2)設Sn為數列{bn}的前n項和,且{Sn}是等比數列,求實數a的值;
(3)當a>0時,求數列{an}的最小項.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第1課時練習卷(解析版) 題型:解答題
若數列{an}滿足an+1=an+an+2(n∈N*),則稱數列{an}為“凸數列”.
(1)設數列{an}為“凸數列”,若a1=1,a2=-2,試寫出該數列的前6項,并求出前6項之和;
(2)在“凸數列”{an}中,求證:an+3=-an,n∈N*;
(3)設a1=a,a2=b,若數列{an}為“凸數列”,求數列前2011項和S2011.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com