
 圓錐曲線上任意兩點連成的線段稱為弦.若圓錐曲線上的一條弦垂直于其對稱軸,我們將該弦稱之為曲線的垂軸弦.已知點P(x0,y0)、M(m,n)是圓錐曲線C上不與頂點重合的任意兩點,MN是垂直于x軸的一條垂軸弦,直線MP、NP分別交x軸于點E(xE,0)和點F(xF,0).
圓錐曲線上任意兩點連成的線段稱為弦.若圓錐曲線上的一條弦垂直于其對稱軸,我們將該弦稱之為曲線的垂軸弦.已知點P(x0,y0)、M(m,n)是圓錐曲線C上不與頂點重合的任意兩點,MN是垂直于x軸的一條垂軸弦,直線MP、NP分別交x軸于點E(xE,0)和點F(xF,0).| x2 |
| a2 |
| y2 |
| b2 |
| m2y02-n2x02 |
| y02-n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| y0-n |
| x0-m |
| my0-nx0 |
| y0-n |
| my0+nx0 |
| y0+n |
| m2y02-n2x02 |
| y02-n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| m2 |
| a2 |
| x02 |
| a2 |
m2b2(1-
| ||||
b2(1-
|
| b2(m2-x02) | ||
|
| m2y02-n2x02 |
| y02-n2 |
| m2(R2-x02)-(R2-m2)x02 |
| (R2-x02)-(R2-m2) |
| R2(m2-x02) |
| (m2-x02) |
| x2 |
| a2 |
| y2 |
| b2 |
| m2y02-n2x02 |
| y02-n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| m2 |
| a2 |
| x02 |
| a2 |
m2b2(
| ||||
b2(
|
| b2(x02-m2) | ||
|
| 2(my02-n2x0) |
| y02-n2 |
| 2(my02-n2x0) |
| y02-n2 |
| 2(m2px0-2pmx0) |
| y02-n2 |


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
 圓錐曲線上任意兩點連成的線段稱為弦.若圓錐曲線上的一條弦垂直于其對稱軸,我們將該弦稱之為曲線的垂軸弦.已知橢圓C:
圓錐曲線上任意兩點連成的線段稱為弦.若圓錐曲線上的一條弦垂直于其對稱軸,我們將該弦稱之為曲線的垂軸弦.已知橢圓C:| x2 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 圓錐曲線上任意兩點連成的線段稱為弦.若圓錐曲線上的一條弦垂直于其對稱軸,我們將該弦稱之為曲線的垂軸弦.已知點P(
圓錐曲線上任意兩點連成的線段稱為弦.若圓錐曲線上的一條弦垂直于其對稱軸,我們將該弦稱之為曲線的垂軸弦.已知點P(| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年上海市徐匯區(qū)高三上學期期末理科數(shù)學卷 題型:解答題
圓錐曲線上任意兩點連成的線段稱為弦。若圓錐曲線上的一條弦垂直于其對稱軸,我們將該弦稱之為曲線的垂軸弦。已知點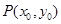 、
、 是圓錐曲線C
是圓錐曲線C 上不與頂點重合的任意兩點,
上不與頂點重合的任意兩點, 是垂直于
是垂直于 軸的一條垂軸弦,直線
軸的一條垂軸弦,直線 分別交
分別交 軸于點
軸于點 和點
和點 。
。

(1)試用 的代數(shù)式分別表示
的代數(shù)式分別表示 和
和 ;
;
(2)若C的方程為 (如圖),求證:
(如圖),求證: 是與
是與 和點
和點 位置無關的定值;
位置無關的定值;
(3)請選定一條除橢圓外的圓錐曲線C,試探究 和
和 經(jīng)過某種四則運算(加、減、乘、除),其
經(jīng)過某種四則運算(加、減、乘、除),其 結果是否是與
結果是否是與 和點
和點 位置無關的定值,寫出你的研究結論并證明。
位置無關的定值,寫出你的研究結論并證明。
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年江蘇省鎮(zhèn)江市揚中二中高三(上)期末數(shù)學模擬試卷(解析版) 題型:解答題
 ”.類比這一結論,我們猜想:“若曲線C的方程為
”.類比這一結論,我們猜想:“若曲線C的方程為 (如圖),則xE•xF也是與點M、N、P位置無關的定值”,請你對該猜想給出證明.
(如圖),則xE•xF也是與點M、N、P位置無關的定值”,請你對該猜想給出證明.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com