
【題目】已知函數![]() ,給出下列結論:
,給出下列結論:
①![]() 的單調遞減區間;
的單調遞減區間;
②當![]() 時,直線y=k與y=f (x)的圖象有兩個不同交點;
時,直線y=k與y=f (x)的圖象有兩個不同交點;
③函數y=f(x)的圖象與![]() 的圖象沒有公共點;
的圖象沒有公共點;
④當![]() 時,函數
時,函數![]() 的最小值為2.
的最小值為2.
其中正確結論的序號是_________
【答案】①③
【解析】
①先求出函數的導數,令導函數小于0,解出即可判斷;②根據函數的單調性畫出函數的圖象,通過圖象讀出即可;③求出f(x)的最大值小于y=x2+1的最小值,從而得到答案;④利用對勾函數即可作出判斷.
解:①f′(x)![]() ,令f′(x)<0,解得:x>1,
,令f′(x)<0,解得:x>1,
∴函數f(x)在(1,+∞)遞減,故①正確;
②∵f(x)在(﹣∞,1)遞增,在(1,+∞)遞減,
∴f(x)max=f(1)![]() ,
,
x→﹣∞時,f(x)→﹣∞,x→+∞時,f(x)→0,
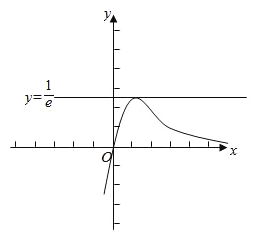
畫出函數f(x)的圖象,如圖示:
 ,
,
∴當k∈(﹣∞,0)時,直線y=k與y=f(x)的圖象有1個不同交點,
當k∈(0,![]() )時,直線y=k與y=f(x)的圖象有兩個不同交點,故②錯誤;
)時,直線y=k與y=f(x)的圖象有兩個不同交點,故②錯誤;
③函數f(x)![]() ,而y=x2+1≥1,
,而y=x2+1≥1,
∴函數y=f(x)的圖象與y=x2+1的圖象沒有公共點,故③正確;
④當![]() 時,令t=
時,令t=![]() ,
,
![]() 在
在![]() 上單調遞減,
上單調遞減,
∴![]() ,最小值不等于2,故④錯誤.
,最小值不等于2,故④錯誤.
故答案為:①③.


科目:高中數學 來源: 題型:
【題目】《中華人民共和國道路交通安全法》第47條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”, 《中華人民共和國道路交通安全法》第90條規定:對不禮讓行人的駕駛員處以扣3分,罰款50元的處罰.下表是某市一主干路口監控設備所抓拍的5個月內駕駛員“禮讓斑馬線”行為統計數據:
月份 | 1 | 2 | 3 | 4 | 5 |
違章駕駛員人數 | 120 | 105 | 100 | 90 | 85 |
(1)請利用所給數據求違章人數![]() 與月份
與月份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ;
;
(2)預測該路口9月份的不“禮讓斑馬線”違章駕駛員人數.
參考公式:  ,
, ![]() .
.
參考數據: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一個特定時段內,以點E為中心的7n mile以內海域被設為警戒水域.點E正北55n mile處有一個雷達觀測站A,某時刻測得一艘勻速直線行駛的船只位于點A北偏東45°且與點A相距40![]() n mile的位置B,經過40分鐘又測得該船已行駛到點A北偏東
n mile的位置B,經過40分鐘又測得該船已行駛到點A北偏東![]() (其中
(其中![]() ,
,![]() )且與點A相距10
)且與點A相距10![]() n mile的位置C.
n mile的位置C.
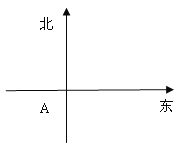
(I)求該船的行駛速度(單位:n mile /h);
(II)若該船不改變航行方向繼續行駛.判斷它是否會進入警戒水域,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學研究性學習是高中學生數學學習的一個有機組成部分,是在基礎性、拓展性課程學習的基礎上,進一步鼓勵學生運用所學知識解決數學的和現實的問題的一種有意義的主動學習,是以學生動手動腦主動探索實踐和相互交流為主要學習方式的學習研究活動.某同學就在一次數學研究性學習中發現,以下五個式子的值都等于同一個常數.
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤![]() .
.
(1)試從上述五個式子中選擇一個,求出這個常數;
(2)根據(1)的計算結果,歸納出一個三角恒等式;
(3)利用所學知識證明這個結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,CM,CN為某公園景觀湖胖的兩條木棧道,∠MCN=120°,現擬在兩條木棧道的A,B處設置觀景臺,記BC=a,AC=b,AB=c(單位:百米)
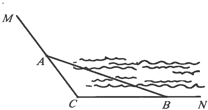
(1)若a,b,c成等差數列,且公差為4,求b的值;
(2)已知AB=12,記∠ABC=θ,試用θ表示觀景路線A-C-B的長,并求觀景路線A-C-B長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的是( )
A.復數z1,z2的模相等,則z1,z2是共軛復數
B.z1,z2都是復數,若z1+z2是虛數,則z1不是z2的共軛復數
C.復數z是實數的充要條件是z=![]() (
(![]() 是z的共軛復數)
是z的共軛復數)
D.已知復數z1=-1+2i,z2=1-i,z3=3-2i(i是虛數單位),它們對應的點分別為A,B,C,O為坐標原點,若![]() (x,y∈R),則x+y=1
(x,y∈R),則x+y=1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代著名的![]() 周髀算經
周髀算經![]() 中提到:凡八節二十四氣,氣損益九寸九分六分分之一;冬至晷
中提到:凡八節二十四氣,氣損益九寸九分六分分之一;冬至晷![]() 長一丈三尺五寸,夏至晷長一尺六寸
長一丈三尺五寸,夏至晷長一尺六寸![]() 意思是:一年有二十四個節氣,每相鄰兩個節氣之間的日影長度差為
意思是:一年有二十四個節氣,每相鄰兩個節氣之間的日影長度差為![]() 分;且“冬至”時日影長度最大,為1350分;“夏至”時日影長度最小,為160分
分;且“冬至”時日影長度最大,為1350分;“夏至”時日影長度最小,為160分![]() 則“立春”時日影長度為
則“立春”時日影長度為![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高級中學今年高一年級招收“國際班”學生![]() 人,學校為這些學生開辟了直升海外一流大學的綠色通道,為了逐步提高這些學生與國際教育接軌的能力,將這
人,學校為這些學生開辟了直升海外一流大學的綠色通道,為了逐步提高這些學生與國際教育接軌的能力,將這![]() 人分為三個批次參加國際教育研修培訓,在這三個批次的學生中男、女學生人數如下表:
人分為三個批次參加國際教育研修培訓,在這三個批次的學生中男、女學生人數如下表:
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 名,抽到第一批次、第二批次中女學生的概率分別是
名,抽到第一批次、第二批次中女學生的概率分別是![]() .
.
(1)求![]() 的值;
的值;
(2)為了檢驗研修的效果,現從三個批次中按分層抽樣的方法抽取![]() 名同學問卷調查,則三個批次被選取的人數分別是多少?
名同學問卷調查,則三個批次被選取的人數分別是多少?
(3)若從第(2)小問選取的學生中隨機選出兩名學生進行訪談,求“參加訪談的兩名同學至少有一個人來自第一批次”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com