
若非零函數 對任意實數
對任意實數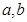 均有
均有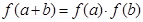 ,且當
,且當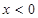 時,
時,  ;
;
(1)求證: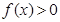 (2)求證:
(2)求證: 為減函數
為減函數
(3)當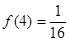 時,解不等式
時,解不等式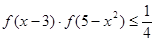
(1)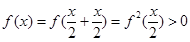 ;
;
(2)見解析;(3)不等式的解集為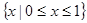 。
。
解析試題分析:(1)利用已知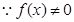
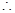
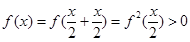 ,可得結論。
,可得結論。
(2)根據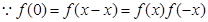 =1,得到f(x)與f(-x)的關系式,進而求解得到。
=1,得到f(x)與f(-x)的關系式,進而求解得到。
(3)由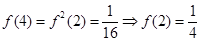 原不等式轉化為
原不等式轉化為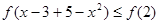 進而結合單調性得到。
進而結合單調性得到。
解:(1)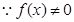
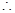
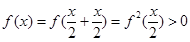 ------------3分
------------3分
(2)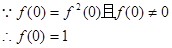 -------------5分
-------------5分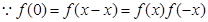
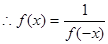 -------------8分
-------------8分
設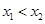 則
則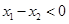
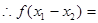
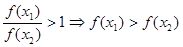 ,
, 為減函數
為減函數
-------10分
(3)由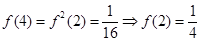 原不等式轉化為
原不等式轉化為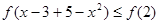 ,結合(2)得:
,結合(2)得: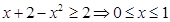
故不等式的解集為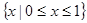 ------------------13分
------------------13分
考點:本題主要考查了函數的性質以及不等式的求解的運用。
點評:解決該試題的關鍵是抽象函數的賦值法思想的運用,判定單調性和f(x)與f(-x)的關系式的運用。


科目:高中數學 來源: 題型:解答題
小王需不定期地在某超市購買同一品種的大米.現有甲、乙兩種不同的采購策略,策略甲:每次購買大米的數量一定;策略乙:每次購買大米的錢數一定.若以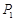 (元)和
(元)和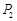 (元)分別記小王先后兩次買米時,該品種大米的單價,請問:僅這兩次買米而言,甲、乙兩種購買方式,從平均單價考慮,哪種比較合算?請進行探討,并給出探討過程.
(元)分別記小王先后兩次買米時,該品種大米的單價,請問:僅這兩次買米而言,甲、乙兩種購買方式,從平均單價考慮,哪種比較合算?請進行探討,并給出探討過程.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某工廠修建一個長方體無蓋蓄水池,其容積為4800立方米,深度為3米.池底每平方米的 造價為150元,池壁每平方米的造價為120元.設池底長方形長為 米.
米.
(1)求底面積,并用含 的表達式表示池壁面積;
的表達式表示池壁面積;
(2)怎樣設計水池能使總造價最低?最低造價是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)
設函數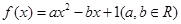 ,
,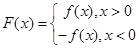
(1) 如果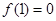 且對任意實數
且對任意實數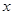 均有
均有 ,求
,求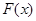 的解析式;
的解析式;
(2) 在(1)在條件下, 若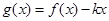 在區間
在區間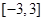 是單調函數,求實數
是單調函數,求實數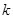 的取值范圍;
的取值范圍;
(3) 已知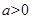 且
且 為偶函數,如果
為偶函數,如果 ,求證:
,求證: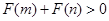 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com