
某工廠的固定成本為3萬元,該工廠每生產100臺某產品的生產成本為1萬元,設生產該產品x(百臺),其總成本為g(x)萬元(總成本=固定成本+生產成本),并且銷售收人r(x)滿足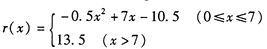 假定該產品產銷平衡,根據上述統計規律求:
假定該產品產銷平衡,根據上述統計規律求:
(1)要使工廠有盈利,產品數量x應控制在什么范圍?
(2)工廠生產多少臺產品時盈利最大?
(1)大于300臺小于1050臺; (2) 600臺
解析試題分析:(1) 由于銷售收入是一個關于產品數量x的一個分段函數,另外計算工廠的盈利需要將銷售收入r(x)減去總的成本g(x)萬元,所以在兩段函數中分別求出盈利大于零的時候產品數量的范圍,及可求得結論.
(2)通過二次函數的最值的求法即可得到盈利最大值時對應的產品數x的值,本小題單位的轉化也是易錯點.
試題解析:依題意得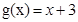 ,設利潤函數為
,設利潤函數為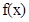 ,則
,則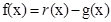 ,
,
所以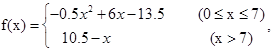 (1)要使工廠有盈利,則有f(x)>0,因為
(1)要使工廠有盈利,則有f(x)>0,因為
f(x)>0?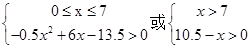 ,
,
⇒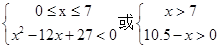 ⇒
⇒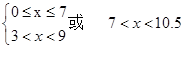
⇒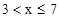 或
或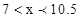 , 即
, 即 .
.
所以要使工廠盈利,產品數量應控制在大于300臺小于1050臺的范圍內
(2)當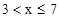 時,
時, 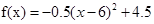
故當x=6時,f(x)有最大值4.5.而當x>7時,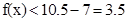 .
.
所以當工廠生產600臺產品時,盈利最大.
考點:1.分段函數的應用.2.函數的最值.3.實際問題的構建數學模型解決.


科目:高中數學 來源: 題型:解答題
設f(x)=|lg x|,a,b為實數,且0<a<b.
(1)求方程f(x)=1的解;
(2)若a,b滿足f(a)=f(b)=2f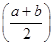 ,
,
求證:a·b=1,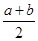 >1.
>1.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對定義域分別是Df,Dg的函數y=f(x),y=g(x),規定:函數h(x)=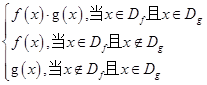
(1)若函數f(x)=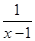 ,g(x)=x2,寫出函數h(x)的解析式;
,g(x)=x2,寫出函數h(x)的解析式;
(2)求問題(1)中函數h(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知兩函數f(x)=8x2+16x-k,g(x)=2x3+5x2+4x,其中k為實數.
(1)對任意x∈[-3,3]都有f(x)≤g(x)成立,求k的取值范圍.
(2)存在x∈[-3,3]使f(x)≤g(x)成立,求k的取值范圍.
(3)對任意x1,x2∈[-3,3]都有f(x1)≤g(x2),求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=ex,x∈R.
(1)若直線y=kx+1與f(x)的反函數的圖像相切,求實數k的值;
(2)設x>0,討論曲線y=f(x)與曲線y=mx2(m>0)公共點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=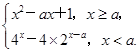
(1)若x<a時,f(x)<1恒成立,求a的取值范圍;
(2)若a≥-4時,函數f(x)在實數集R上有最小值,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廠生產某種產品的年固定成本為250萬元,每生產x千件,需另投入成本為C(x).當年產量不足80千件時,C(x)= x2+10x(萬元);當年產量不小于80千件時,C(x)=51x+
x2+10x(萬元);當年產量不小于80千件時,C(x)=51x+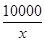 -1 450(萬元),每件商品售價為0.05萬元,通過市場分析,該廠生產的商品能全部售完.
-1 450(萬元),每件商品售價為0.05萬元,通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤L(萬元)關于年產量x(千件)的函數解析式;
(2)當年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 的定義域為
的定義域為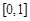 ,且
,且 的圖象連續不間斷. 若函數
的圖象連續不間斷. 若函數 滿足:對于給定的
滿足:對于給定的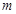 (
(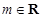 且
且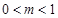 ),存在
),存在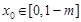 ,使得
,使得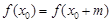 ,則稱
,則稱 具有性質
具有性質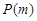 .
.
(1)已知函數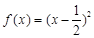 ,
,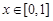 ,判斷
,判斷 是否具有性質
是否具有性質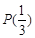 ,并說明理由;
,并說明理由;
(2)已知函數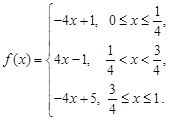 若
若 具有性質
具有性質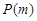 ,求
,求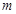 的最大值;
的最大值;
(3)若函數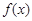 的定義域為
的定義域為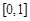 ,且
,且 的圖象連續不間斷,又滿足
的圖象連續不間斷,又滿足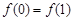 ,
,
求證:對任意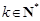 且
且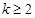 ,函數
,函數 具有性質
具有性質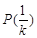 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com