
已知定點A(0,-1),點B在圓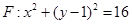 上運動,
上運動,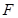
為圓心,線段AB的垂直平分線交BF于P.
(1)求動點P的軌跡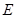 的方程;若曲線
的方程;若曲線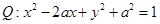 被軌跡
被軌跡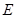 包圍著,求實數(shù)
包圍著,求實數(shù)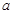 的最小值.
的最小值.
(2)已知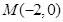 、
、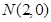 ,動點
,動點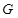 在圓
在圓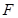 內(nèi),且滿足
內(nèi),且滿足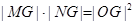 ,求
,求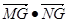 的取值范圍.
的取值范圍.
(1)
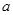 的最小值為
的最小值為 (2)
(2) 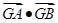 的取值范圍為
的取值范圍為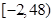
【解析】本試題主要是考查了橢圓方程的求解借助于橢圓的定義得到結(jié)論。然后結(jié)合向量的關系式得到坐標關系,然后利用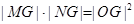 ,得到范圍。
,得到范圍。
(1)由題意得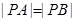 ,∴
,∴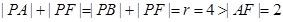
∴P點軌跡是以A、F為焦點的橢圓,進而得到結(jié)論。而曲線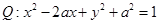 化為
化為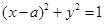 ,
,
則曲線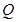 是圓心在
是圓心在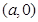 ,半徑為1的圓。
,半徑為1的圓。
,那么利用圖像法得到最值。
(2)設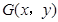 ,由
,由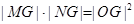 得:
得: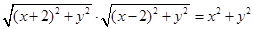 ,
,
化簡得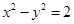 ,即
,即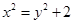 ,
,
而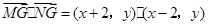
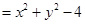
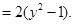
∵點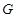 在圓
在圓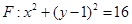 內(nèi),∴
內(nèi),∴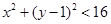 ,得到不等式,然后求解得到。
,得到不等式,然后求解得到。
解:(1)由題意得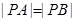 ,∴
,∴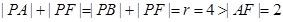
∴P點軌跡是以A、F為焦點的橢圓. ………………………3分
設橢圓方程為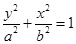
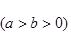 ,
,
則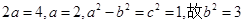 ,
,
∴點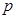 的軌跡方程為
的軌跡方程為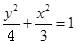 ………………5分
………………5分
曲線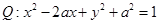 化為
化為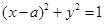 ,
,
則曲線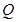 是圓心在
是圓心在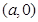 ,半徑為1的圓。
,半徑為1的圓。
而軌跡E: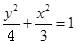 為焦點在y軸上的橢圓短軸上的頂點為
為焦點在y軸上的橢圓短軸上的頂點為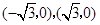 結(jié)合它們的圖像知:
結(jié)合它們的圖像知:
若曲線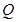 被軌跡E包圍著,則
被軌跡E包圍著,則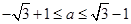 ,
,
∴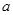 的最小值為
的最小值為 。………………………8分
。………………………8分
(2)設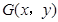 ,由
,由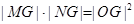 得:
得: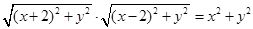 ,
,
化簡得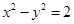 ,即
,即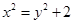 ,
,
而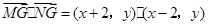
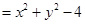
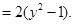 …………10分
…………10分
∵點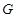 在圓
在圓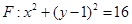 內(nèi),∴
內(nèi),∴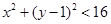
∴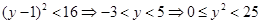 ,
,
∴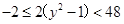 ,
,
∴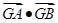 的取值范圍為
的取值范圍為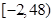 .……………12分
.……………12分


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數(shù)學 來源:訓練必修二數(shù)學蘇教版 蘇教版 題型:022
已知定點A(0,1),點B在直線x+y=0上運動,當線段AB最短時,點B的坐標是________.
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年廣東省肇慶市高三數(shù)學復習必修2模塊測試試卷D卷 題型:填空題
已知定點A(0,1),點B在直線x+y=0上運動,當線段AB最短時,點B的坐標是___________________.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com