
【題目】設(shè)函數(shù)![]() ,曲線
,曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)求過曲線![]() 上任意一點(diǎn)的切線與直線
上任意一點(diǎn)的切線與直線![]() 和直線
和直線![]() 所圍成的三角形面積.
所圍成的三角形面積.
【答案】(1)![]() ;(2)6
;(2)6
【解析】
(1)直接根據(jù)切線方程公式得到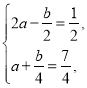 ,解得答案.
,解得答案.
(2)設(shè)![]() 為曲線上任一點(diǎn),切線方程為
為曲線上任一點(diǎn),切線方程為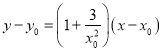 ,計算切線與直線
,計算切線與直線![]() 的交點(diǎn)坐標(biāo)為
的交點(diǎn)坐標(biāo)為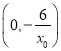 ,與直線y=x的交點(diǎn)坐標(biāo)為(2x0,2x0),計算面積得到答案.
,與直線y=x的交點(diǎn)坐標(biāo)為(2x0,2x0),計算面積得到答案.
(1)方程![]() 可化為
可化為![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,又
,又![]() ,
,
于是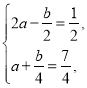 解得
解得![]() ,故
,故![]() .
.
(2)設(shè)![]() 為曲線上任一點(diǎn),由
為曲線上任一點(diǎn),由![]() 知:
知:
![]() 處的切線方程為
處的切線方程為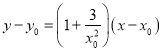 ,
,
即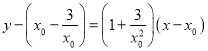 .令
.令![]() ,得
,得![]() ,
,
從而得切線與直線![]() 的交點(diǎn)坐標(biāo)為
的交點(diǎn)坐標(biāo)為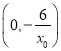 .
.
令y=x,得y=x=2x0,從而得切線與直線y=x的交點(diǎn)坐標(biāo)為(2x0,2x0);
點(diǎn)P(x0,y0)處的切線與直線x=0,y=x,所圍成的三角形面積為![]() |﹣
|﹣![]() ||2x0|=6.
||2x0|=6.


 53隨堂測系列答案
53隨堂測系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近兩年來,以《中國詩詞大會》為代表的中國文化類電視節(jié)目帶動了一股中國文化熱潮.某臺舉辦闖關(guān)答題比賽,共分兩輪,每輪共有4類題型,選手從前往后逐類回答,若中途回答錯誤,立馬淘汰,若全部回答正確,就能獲得一枚復(fù)活幣并進(jìn)行下一輪答題,兩輪都通過就可以獲得最終獎金.選手在第一輪闖關(guān)獲得的復(fù)活幣,系統(tǒng)會在下一輪答題中自動使用,即下一輪重新進(jìn)行闖關(guān)答題時,在某一類題型中回答錯誤,自動復(fù)活一次,視為答對該類題型.若某選手每輪的4類題型的通過率均分別為![]() 、
、![]() 、
、![]() 、
、![]() ,則該選手進(jìn)入第二輪答題的概率為_________;該選手最終獲得獎金的概率為_________.
,則該選手進(jìn)入第二輪答題的概率為_________;該選手最終獲得獎金的概率為_________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)從某醫(yī)院中隨機(jī)抽取了![]() 位醫(yī)護(hù)人員的關(guān)愛患者考核分?jǐn)?shù)(患者考核:
位醫(yī)護(hù)人員的關(guān)愛患者考核分?jǐn)?shù)(患者考核:![]() 分制),用相關(guān)的特征量
分制),用相關(guān)的特征量![]() 表示;醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)(試卷考試:
表示;醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)(試卷考試:![]() 分制),用相關(guān)的特征量
分制),用相關(guān)的特征量![]() 表示,數(shù)據(jù)如下表:
表示,數(shù)據(jù)如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程(計算結(jié)果精確到
的線性回歸方程(計算結(jié)果精確到![]() );
);
(2)利用(1)中的線性回歸方程,分析醫(yī)護(hù)專業(yè)考核分?jǐn)?shù)的變化對關(guān)愛患者考核分?jǐn)?shù)的影響,并估計當(dāng)某醫(yī)護(hù)人員的醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)為![]() 分時,他的關(guān)愛患者考核分?jǐn)?shù)(精確到
分時,他的關(guān)愛患者考核分?jǐn)?shù)(精確到![]() ).
).
參考公式及數(shù)據(jù):回歸直線方程![]() 中斜率和截距的最小二乘法估計公式分別為
中斜率和截距的最小二乘法估計公式分別為
 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題正確的有_________(填序號)
①已知![]() :
:![]() 或
或![]() ,
,![]() :
:![]() ,則
,則![]() 是
是![]() 的必要不充分條件;
的必要不充分條件;
②“![]() ”是“函數(shù)
”是“函數(shù)![]() 的最小正周期為
的最小正周期為![]() ”的充分不必要條件;
”的充分不必要條件;
③![]() 中,內(nèi)角
中,內(nèi)角![]() ,
,![]() ,
,![]() 所對的邊分別為
所對的邊分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則“
,則“![]() ”是“
”是“![]() 為等腰三角形”的必要不充分條件;
為等腰三角形”的必要不充分條件;
④若命題![]() :“函數(shù)
:“函數(shù)![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ”為真命題,則實(shí)數(shù)
”為真命題,則實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,點(diǎn)
,點(diǎn)![]() 在第一象限,以
在第一象限,以![]() 為直徑的圓與
為直徑的圓與![]() 軸相切,動點(diǎn)
軸相切,動點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線的斜率為
處的切線的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求滿足
,求滿足![]() 的點(diǎn)
的點(diǎn)![]() 的個數(shù).
的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,過點(diǎn)
,過點(diǎn)![]() 且與
且與![]() 軸垂直的直線被橢圓截得的線段長為
軸垂直的直線被橢圓截得的線段長為![]() ,且
,且![]() 與短軸兩端點(diǎn)的連線相互垂直.
與短軸兩端點(diǎn)的連線相互垂直.
(1)求橢圓![]() 的方程;
的方程;
(2)若圓![]() 上存在兩點(diǎn)
上存在兩點(diǎn)![]() ,
,![]() ,橢圓
,橢圓![]() 上存在兩個點(diǎn)
上存在兩個點(diǎn)![]() 滿足:
滿足:![]() 三點(diǎn)共線,
三點(diǎn)共線,![]() 三點(diǎn)共線,且
三點(diǎn)共線,且![]() ,求四邊形
,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為迎接國慶匯演,學(xué)校擬對參演的班級進(jìn)行獎勵性加分表彰,每選中一個節(jié)目,其班級量化考核積分加3分.某班級準(zhǔn)備了三個文娛節(jié)目,這三個節(jié)目被選中的概率分別為![]() ,
,![]() ,
,![]() ,且每個節(jié)目是否被選中是相互獨(dú)立的.
,且每個節(jié)目是否被選中是相互獨(dú)立的.
(1)求該班級被加分的概率;
(2)求該班級獲得獎勵性積分![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】比較甲、乙兩名學(xué)生的數(shù)學(xué)學(xué)科素養(yǎng)的各項(xiàng)能力指標(biāo)值(滿分為5分,分值高者為優(yōu)),繪制了如圖1所示的六維能力雷達(dá)圖,例如圖中甲的數(shù)學(xué)抽象指標(biāo)值為4,乙的數(shù)學(xué)抽象指標(biāo)值為5,則下面敘述正確的是( )
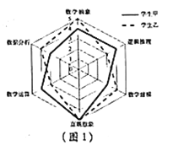
A. 乙的邏輯推理能力優(yōu)于甲的邏輯推理能力
B. 甲的數(shù)學(xué)建模能力指標(biāo)值優(yōu)于乙的直觀想象能力指標(biāo)值
C. 乙的六維能力指標(biāo)值整體水平優(yōu)于甲的六維能力指標(biāo)值整體水平
D. 甲的數(shù)學(xué)運(yùn)算能力指標(biāo)值優(yōu)于甲的直觀想象能力指標(biāo)值
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com