
【題目】“綠水青山就是金山銀山”,為了響應國家政策,我市環保部門對市民進行了一次環境保護知識的網絡問卷調查,每位市民僅有一次參加機會,通過隨機抽樣,得到參與問卷調查的50人的得分(滿分:100分)數據,統計結果如表所示:
組別 |
|
|
|
|
|
|
男 | 1 | 2 | 2 | 10 | 9 | 6 |
女 | 0 | 5 | 5 | 5 | 3 | 2 |
若規定問卷得分不低于70分的市民稱為“環境保護關注者”,則上圖中表格可得![]() 列聯表如下:
列聯表如下:
非“環境保護關注者” | 是“環境保護關注者” | 合計 | |
男 | 5 | 25 | 30 |
女 | 10 | 10 | 20 |
合計 | 15 | 35 | 50 |
(1)請完成上述![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為“環境保護關注者”與性別有關?
列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為“環境保護關注者”與性別有關?
(2)若問卷得分不低于80分的人稱為“環境保護達人”,現在從本次調查的“環境保護達人”中利用分層抽樣的方法抽取4名市民參與環保知識問答,再從這4名市民中隨機抽取2人參與座談會,求抽取的2名市民中,既有男“環境保護達人”又有女“環境保護達人”的概率.
附表及公式: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】![]()
![]() 列聯表見解析,在犯錯誤的概率不超過0.05的前提下認為“環境保護關注者”與性別有關;
列聯表見解析,在犯錯誤的概率不超過0.05的前提下認為“環境保護關注者”與性別有關;![]()
![]()
【解析】
![]() 根據表中的數據重新整合,完成
根據表中的數據重新整合,完成![]() 列聯表,然后將列聯表中的數據代入
列聯表,然后將列聯表中的數據代入![]() 的公式計算求解,結合臨界值表進行判斷即可;
的公式計算求解,結合臨界值表進行判斷即可;
![]() 列舉出所有可能的情況和既有男“環境保護達人”又有女“環境保護達人”包含的情況,再利用古典概型的概率計算公式求解即可.
列舉出所有可能的情況和既有男“環境保護達人”又有女“環境保護達人”包含的情況,再利用古典概型的概率計算公式求解即可.
![]() 由表中數據可得
由表中數據可得![]() 列聯表如下,
列聯表如下,
非“環境保護關注者” | 是“環境保護關注者” | 合計 | |
男 | 5 | 25 | 30 |
女 | 10 | 10 | 20 |
合計 | 15 | 35 | 50 |
將![]() 列聯表中的數據代入公式可得,
列聯表中的數據代入公式可得,
![]() 的觀測值
的觀測值![]() ,
,
所以在犯錯誤的概率不超過0.05的前提下認為“環境保護關注者”與性別有關;
![]() 由題可知,利用分層抽樣的方法可得,
由題可知,利用分層抽樣的方法可得,
抽取4名市民中男環保達人![]() 人,女環保達人
人,女環保達人![]() 人,
人,
設男環保達人為![]() ,女環保達人為
,女環保達人為![]() ,
,
從中抽取兩人參與座談會所有的情況為
![]() 共
共![]() 種情況,
種情況,
既有男“環境保護達人”又有女“環境保護達人”包含的情況為
![]() 共
共![]() 種情況,
種情況,
由古典概型的概率計算公式可得,
所求概率![]() .
.


 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,從流水線上隨機抽取![]() 件產品,統計其質量指標值并繪制頻率分布直方圖(如圖1):規定產品的質量指標值在
件產品,統計其質量指標值并繪制頻率分布直方圖(如圖1):規定產品的質量指標值在![]() 的為劣質品,在
的為劣質品,在![]() 的為優等品,在
的為優等品,在![]() 的為特優品,銷售時劣質品每件虧損
的為特優品,銷售時劣質品每件虧損![]() 元,優等品每件盈利
元,優等品每件盈利![]() 元,特優品每件盈利
元,特優品每件盈利![]() 元,以這
元,以這![]() 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
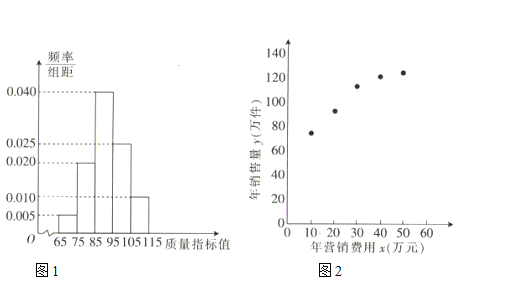
(1)求每件產品的平均銷售利潤;
(2)該企業主管部門為了解企業年營銷費用![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:萬件)的影響,對該企業近
(單位:萬件)的影響,對該企業近![]() 年的年營銷費用
年的年營銷費用![]() 和年銷售量
和年銷售量![]() ,
,![]() 數據做了初步處理,得到的散點圖(如圖2)及一些統計量的值.
數據做了初步處理,得到的散點圖(如圖2)及一些統計量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根據散點圖判斷,![]() 可以作為年銷售量
可以作為年銷售量![]() (萬件)關于年營銷費用
(萬件)關于年營銷費用![]() (萬元)的回歸方程.
(萬元)的回歸方程.
①求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②用所求的回歸方程估計該企業每年應投入多少營銷費,才能使得該企業的年收益的預報值達到最大?(收益![]() 銷售利潤
銷售利潤![]() 營銷費用,取
營銷費用,取![]() )
)
附:對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為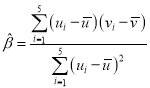 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】去年年底,某商業集團公司根據相關評分細則,對其所屬25家商業連鎖店進行了考核評估.將各連鎖店的評估分數按[60,70), [70,80), [80,90), [90,100),分成四組,其頻率分布直方圖如下圖所示,集團公司依據評估得分,將這些連鎖店劃分為A,B,C,D四個等級,等級評定標準如下表所示.
評估得分 | [60,70) | [70,80) | [80,90) | [90,100) |
評定等級 | D | C | B | A |

(1)估計該商業集團各連鎖店評估得分的眾數和平均數;
(2)從評估分數不小于80分的連鎖店中任選2家介紹營銷經驗,求至少選一家A等級的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年在印度尼西亞日惹舉辦的亞洲乒乓球錦標賽男子團體決賽中,中國隊與韓國隊相遇,中國隊男子選手A,B,C,D,E依次出場比賽,在以往對戰韓國選手的比賽中他們五人獲勝的概率分別是0.8,0.8,0.8,0.75,0.7,并且比賽勝負相互獨立.賽會釆用5局3勝制,先贏3局者獲得勝利.
(1)在決賽中,中國隊以3∶1獲勝的概率是多少?
(2)求比賽局數的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年底,北京2022年冬奧組委會啟動志愿者全球招募,僅一個月內報名人數便突破60萬,其中青年學生約有50萬人.現從這50萬青年學生志愿者中,按男女分層抽樣隨機選取20人進行英語水平測試,所得成績(單位:分)統計結果用莖葉圖記錄如下:

(Ⅰ)試估計在這50萬青年學生志愿者中,英語測試成績在80分以上的女生人數;
(Ⅱ)從選出的8名男生中隨機抽取2人,記其中測試成績在70分以上的人數為X,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)為便于聯絡,現將所有的青年學生志愿者隨機分成若干組(每組人數不少于5000),并在每組中隨機選取![]() 個人作為聯絡員,要求每組的聯絡員中至少有1人的英語測試成績在70分以上的概率大于90%.根據圖表中數據,以頻率作為概率,給出
個人作為聯絡員,要求每組的聯絡員中至少有1人的英語測試成績在70分以上的概率大于90%.根據圖表中數據,以頻率作為概率,給出![]() 的最小值.(結論不要求證明)
的最小值.(結論不要求證明)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com