
【題目】若規定E={a1 , a2 , …,a10}的子集{at1 , at2 , …,ak}為E的第k個子集,其中 ![]() ,則E的第211個子集是 .
,則E的第211個子集是 .
【答案】{a1,a2,a5,a7,a8}
【解析】解:∵27=128<211,而28=256>211,
∴E的第211個子集包含a8,
此時211﹣128=83,
∵26=64<83,27=128>83,
∴E的第211個子集包含a7,
此時83﹣64=19,
∵24=16<19,25=32>19,
∴E的第211個子集包含a5,
此時19﹣16=3
∵21<3,22=4>3,
∴E的第211個子集包含a2,
此時3﹣2=1,20=1,
∴E的第211個子集包含a1.
∴E的第211個子集是{a1,a2,a5,a7,a8};
所以答案是:{a1,a2,a5,a7,a8}.
【考點精析】關于本題考查的子集與真子集,需要了解任何一個集合是它本身的子集;n個元素的子集有2n個,n個元素的真子集有2n -1個,n個元素的非空真子集有2n-2個才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】為了緩解交通壓力,某省在兩個城市之間特修一條專用鐵路,用一列火車作為公共交通車.已知每日來回趟數y是每次拖掛車廂節數x的一次函數,如果該列火車每次拖4節車廂,每日能來回16趟;如果每次拖6節車廂,則每日能來回10趟,火車每日每次拖掛車廂的節數是相同的,每節車廂滿載時能載客110人.
(1)求出y關于x的函數;
(2)該火車滿載時每次拖掛多少節車廂才能使每日營運人數最多?并求出每天最多的營運人數?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,給出下列結論:
,給出下列結論:
(1)若對任意![]() ,且
,且![]() ,都有
,都有![]() ,則
,則![]() 為R上的減函數;
為R上的減函數;
(2)若![]() 為R上的偶函數,且在
為R上的偶函數,且在![]() 內是減函數,
內是減函數, ![]() (-2)=0,則
(-2)=0,則![]() >0解集為(-2,2);
>0解集為(-2,2);
(3)若![]() 為R上的奇函數,則
為R上的奇函數,則![]() 也是R上的奇函數;
也是R上的奇函數;
(4)t為常數,若對任意的![]() ,都有
,都有![]() 則
則![]() 關于
關于![]() 對稱。
對稱。
其中所有正確的結論序號為_________
查看答案和解析>>
科目:高中數學 來源: 題型:
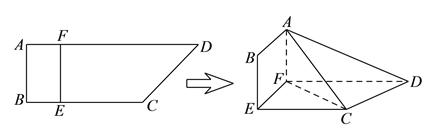
【題目】如圖,四邊形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,
上, ![]() ,現將四邊形
,現將四邊形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,是否存在折疊后的線段
,是否存在折疊后的線段![]() 上存在一點
上存在一點![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
(![]() )求三棱錐
)求三棱錐![]() 的體積的最大值,并求此時點
的體積的最大值,并求此時點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,多面體PABCD的直觀圖及三視圖如圖所示,E、F分別為PC、BD的中點.

(I)求證:EF∥平面PAD;
(II)求證:平面PDC⊥平面PAD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() ,g(x)=lnx+
,g(x)=lnx+ ![]() (a>0).
(a>0).
(1)求函數f(x)的極值;
(2)若x1、x2∈(0,+∞),使得g(x1)≤f(x2)成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=lnx+ ![]() ,g(x)=ex﹣
,g(x)=ex﹣ ![]() (e是自然對數的底數,a∈R).
(e是自然對數的底數,a∈R).
(Ⅰ)求證:|f(x)|≥﹣(x﹣1)2+ ![]() ;
;
(Ⅱ)已知[x]表示不超過x的最大整數,如[1.9]=1,[﹣2.1]=﹣3,若對任意x1≥0,都存在x2>0,使得g(x1)≥[f(x2)]成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com