
本小題滿分12分)
今有一長2米寬1米的矩形鐵皮,如圖,在四個角上分別截去一個邊長為x米的正方形后,沿虛線折起可做成一個無蓋的長方體形水箱(接口連接問題不考慮).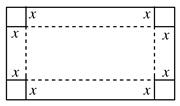
(Ⅰ)求水箱容積的表達式 ,并指出函數
,并指出函數 的定義域;
的定義域;
(Ⅱ)若要使水箱容積不大于 立方米的同時,又使得底面積最大,求x的值.
立方米的同時,又使得底面積最大,求x的值.
(1) {x|0<x< } (2)
} (2) 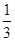
解析試題分析:解:(Ⅰ)由已知該長方體形水箱高為x米,底面矩形長為(2-2x)米,寬(1-2x)米.
∴該水箱容積為
f(x)=(2-2x)(1-2x)x=4x3-6x2+2x. ………………………4分
其中正數x滿足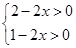 ∴0<x<
∴0<x< .
.
∴所求函數f(x)定義域為{x|0<x< }.………………………6分
}.………………………6分
(Ⅱ)由f(x)≤4x3,得x ≤ 0或x ≥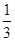 ,
,
∵定義域為{x|0<x< },∴
},∴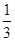 ≤ x<
≤ x< .………………………8分
.………………………8分
此時的底面積為S(x)=(2-2x)(1-2x)=4x2-6x+2
(x∈[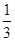 ,
, )).由S(x)=4(x-
)).由S(x)=4(x-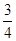 )2-
)2-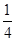 ,………………………10分
,………………………10分
可知S(x)在[ 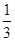 ,
, )上是單調減函數,
)上是單調減函數,
∴x=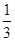 .即滿足條件的x是
.即滿足條件的x是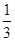 .………………………12分
.………………………12分
考點:本試題考查了函數的實際運用。
點評:對于實際運用題,要準確的審清題意,并能抽象出函數關系式,然后結合分段函數的性質來分析定義域和單調性,以及求解最值的問題。注意實際問題中,變量的范圍確定,要符合實際意義,屬于中檔題。


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案科目:高中數學 來源: 題型:解答題
(本題滿分12分)
一次函數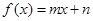 與指數型函數
與指數型函數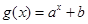 ,(
,(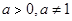 )的圖像交于兩點
)的圖像交于兩點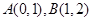 ,解答下列各題
,解答下列各題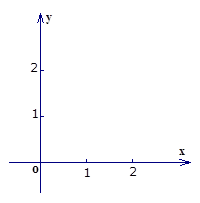 :
:
(1)求一次函數 和指數型函數
和指數型函數 的表達式;
的表達式;
(2)作出這兩個函數的圖像;
(3)填空:當 時,
時,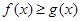 ;當
;當 時,
時,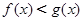 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數 的最小值為1,且
的最小值為1,且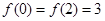 。
。
(1)求 的解析式;
的解析式;
(2)若 在區間
在區間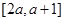 上不單調,求實數
上不單調,求實數 的取值范圍;
的取值范圍;
(3)在區間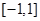 上,
上,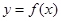 的圖象恒在
的圖象恒在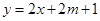 的圖象上方,試確定實數
的圖象上方,試確定實數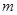 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com