
已知二次函數f(x)=ax2+bx,f(x+1)為偶函數,函數f(x)的圖象與直線y=x相切.
(I)求f(x)的解析式;
(II)已知k的取值范圍為[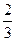 ,+∞),則是否存在區間[m,n](m<n),使得f(x)在區間[m,n]上的值域恰好為[km,kn]?若存在,請求出區間[m,n];若不存在,請說明理由.
,+∞),則是否存在區間[m,n](m<n),使得f(x)在區間[m,n]上的值域恰好為[km,kn]?若存在,請求出區間[m,n];若不存在,請說明理由.
解:(1)∵f(x+1)為偶函數,∴f(-x+1)=f(x+1),
即a(-x+1)2+b(-x+1)=a(x+1)2+b(x+1)恒成立,
即(2a+b)x=0恒成立,∴2a+b=0,∴b=-2a,∴f(x)=ax2-2ax,
∵函數f(x)的圖象與直線y=x相切,
∴二次方程ax2-(2a+1)x=0有兩相等實數根,∴Δ=(2a+1)2-4a×0=0,
∴a=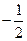 ,f(x)=-
,f(x)=-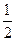 x2+x. ......5分
x2+x. ......5分
(2)∵f(x)=-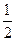 (x-1)2+
(x-1)2+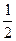 ≤
≤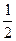 ,
,
∴[km,kn]⊆(-∞,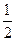 ],∴kn≤
],∴kn≤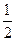 ,又k≥
,又k≥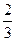 ,∴n≤
,∴n≤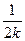 ≤
≤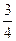 ,
,
又[m,n]⊆ (-∞,1],f(x)在[m,n]上是單調增函數,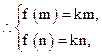 即-
即-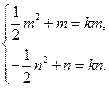
即m,n為方程-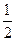 x2+x=kx的兩根,解得x1=0,x2=2-2k.∵m<n且k≥
x2+x=kx的兩根,解得x1=0,x2=2-2k.∵m<n且k≥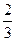 .
.
故當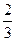 ≤k<1時,[m,n]="[0,2-2k];" 當k>1時,[m,n]=[2-2k,0]; 當k=1時,[m,n]不存在.
≤k<1時,[m,n]="[0,2-2k];" 當k>1時,[m,n]=[2-2k,0]; 當k=1時,[m,n]不存在.
解析


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:解答題
汽車和自行車分別從 地和
地和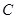 地同時開出,如下圖,各沿箭頭方向(兩方向垂直)勻速前進,汽車和自行車的速度分別是10米/秒和5米/秒,已知
地同時開出,如下圖,各沿箭頭方向(兩方向垂直)勻速前進,汽車和自行車的速度分別是10米/秒和5米/秒,已知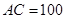 米.(汽車開到
米.(汽車開到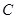 地即停止)
地即停止)
(Ⅰ)經過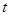 秒后,汽車到達
秒后,汽車到達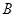 處,自行車到達
處,自行車到達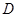 處,設
處,設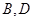 間距離為
間距離為 ,試寫出
,試寫出 關于
關于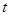 的函數關系式,并求其定義域.
的函數關系式,并求其定義域.
(Ⅱ)經過多少時間后,汽車和自行車之間的距離最短?最短距離是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分)某企業擬在2012年度進行一系列促銷活動,已知某產品年銷量x萬件與年促銷費用t萬元之間滿足3-x與t+1成反比例,當年促銷費用t=0萬元時,年銷量是1萬件,已知2012年產品的設備折舊、維修等固定費用為3萬元,每生產1萬件產品需再投入32萬元的生產費用。若將每件產品售價定為:其生產成本的150%與“平均每件促銷費的一半”之和,則當年生產的商
(1)將2012年的利潤y(萬元)表示為促銷費t(萬元)的函數
(2)該企業2012年的促銷費投入多少萬元時,企業年利潤最大?(注:利潤=銷售收入-生產成
本-促銷費,生產成本=固定費用+生產費用)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
.(本小題滿分12分)
某服裝廠生產一種服裝,每件服裝的成本為40元,出廠單價定為60元.該廠為鼓勵銷售商訂購,決定當一次訂購量超過100件時,每多訂購一件,訂購的全部服裝的出廠單價就降低0.02元.根據市場調查,銷售商一次訂購量不會超過500件.
(1)設一次訂購量為x件,服裝的實際出廠單價為P元,寫出函數P=f(x)的表達式;
(2)當銷售商一次訂購多少件時,該服裝廠獲得的利潤最大,最大利潤是多少元?
(服裝廠售出一件服裝的利潤=實際出廠單價 成本)
成本)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com