
已知函數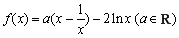 .
.
(Ⅰ)若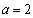 ,求曲線
,求曲線 在點
在點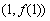 處的切線方程;
處的切線方程;
(Ⅱ)求函數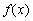 的單調區間;
的單調區間;
(Ⅲ)設函數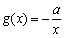 .若至少存在一個
.若至少存在一個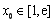 ,使得
,使得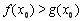 成立,求實數
成立,求實數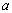 的取值范圍.
的取值范圍.
(Ⅰ) (Ⅱ)單調遞增區間為
(Ⅱ)單調遞增區間為 和
和 ,
,
單調遞減區間為 (Ⅲ)
(Ⅲ)
【解析】函數的定義域為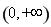 ,
, .………1分
.………1分
(Ⅰ)當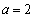 時,函數
時,函數 ,
, ,
, .
.
所以曲線 在點
在點 處的切線方程為
處的切線方程為 ,
,
即 .………………………3分
.………………………3分
(Ⅱ)函數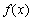 的定義域為
的定義域為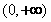 .
.
(1)當 時,
時, 在
在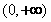 上恒成立,
上恒成立,
則 在
在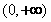 上恒成立,此時
上恒成立,此時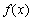 在
在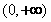 上單調遞減. ……………4分
上單調遞減. ……………4分
(2)當 時,
時, ,
,
(ⅰ)若 ,
,
由 ,即
,即 ,得
,得 或
或 ; ………………5分
; ………………5分
由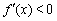 ,即
,即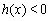 ,得
,得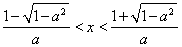 .………………………6分
.………………………6分
所以函數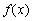 的單調遞增區間為
的單調遞增區間為 和
和 ,
,
單調遞減區間為 . ……………………………………7分
. ……………………………………7分
(ⅱ)若 ,
, 在
在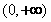 上恒成立,則
上恒成立,則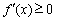 在
在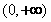 上恒成立,此時
上恒成立,此時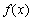 在
在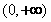 上單調遞增. ………………………………………………………………8分
上單調遞增. ………………………………………………………………8分
(Ⅲ))因為存在一個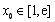 使得
使得 ,
,
則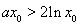 ,等價于
,等價于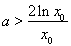 .…………………………………………………9分
.…………………………………………………9分
令 ,等價于“當
,等價于“當 時,
時, ”.
”.
對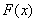 求導,得
求導,得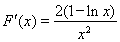 .……………………………………………10分
.……………………………………………10分
因為當 時,
時, ,所以
,所以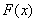 在
在 上單調遞增. ……………12分
上單調遞增. ……………12分
所以 ,因此
,因此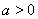 . …………………………………………13分
. …………………………………………13分
另【解析】
設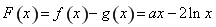 ,定義域為
,定義域為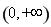 ,
,
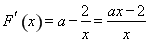 .
.
依題意,至少存在一個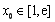 ,使得
,使得 成立,
成立,
等價于當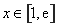 時,
時, . ………………………………………9分
. ………………………………………9分
(1)當 時,
時,
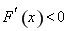 在
在 恒成立,所以
恒成立,所以 在
在 單調遞減,只要
單調遞減,只要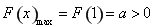 ,
,
則不滿足題意.…… 10分
(2)當 時,令
時,令 得
得 .
.
(ⅰ)當 ,即
,即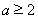 時,
時,
在 上
上 ,所以
,所以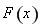 在
在 上單調遞增,
上單調遞增,
所以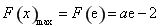 ,由
,由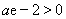 得,
得, ,所以
,所以 .………11分
.………11分
(ⅱ)當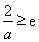 ,即
,即 時,
時,
在 上
上 ,所以
,所以 在
在 單調遞減,
單調遞減,
所以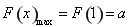 ,由
,由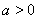 得
得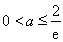 .………………12分
.………………12分
(ⅲ)當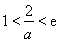 ,即
,即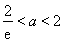 時, 在
時, 在 上
上 ,在
,在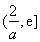 上
上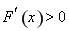 ,
,
所以 在
在 單調遞減,在
單調遞減,在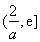 單調遞增,
單調遞增,
 ,等價于
,等價于 或
或 ,解得
,解得 ,所以,
,所以,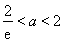 .
.
綜上所述,實數 的取值范圍為
的取值范圍為 .………………………………………13分
.………………………………………13分


科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十三第十章第十節練習卷(解析版) 題型:選擇題
下面是2×2列聯表:
| y1 | y2 | 總計 |
x1 | a | 21 | 73 |
x2 | 22 | 25 | 47 |
總計 | b | 46 | 120 |
則表中a,b的值分別為( )
(A)94,72 (B)52,50
(C)52,74 (D)74,52
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知函數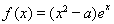 .
.
(Ⅰ)若函數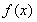 在
在 上不是單調函數,求實數
上不是單調函數,求實數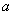 的取值范圍;
的取值范圍;
(Ⅱ)當 時,討論函數
時,討論函數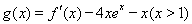 的零點個數.
的零點個數.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知函數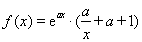 ,其中
,其中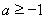 .
.
(Ⅰ)當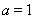 時,求曲線
時,求曲線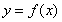 在點
在點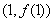 處的切線方程;
處的切線方程;
(Ⅱ)求f(x)的單調區間.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知函數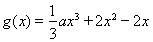 ,函數
,函數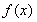 是函數
是函數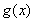 的導函數.
的導函數.
(1)若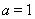 ,求
,求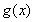 的單調減區間;
的單調減區間;
(2)若對任意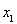 ,
,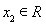 且
且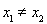 ,都有
,都有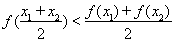 ,求實數
,求實數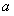 的取值范圍;
的取值范圍;
(3)在第(2)問求出的實數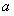 的范圍內,若存在一個與
的范圍內,若存在一個與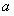 有關的負數
有關的負數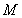 ,使得對任意
,使得對任意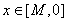 時
時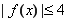 恒成立,求
恒成立,求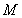 的最小值及相應的
的最小值及相應的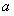 值.
值.
查看答案和解析>>
科目:高中數學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數學試卷(解析版) 題型:選擇題
執行如圖所示的程序框圖,輸入的N=2014,則輸出的S=( )
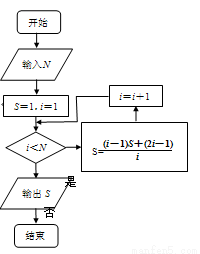
A.2011 B.2012 C.2013 D.2014
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com