
(本小題滿分12分)
如圖,正方體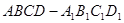 中, E是
中, E是 的中點.
的中點. 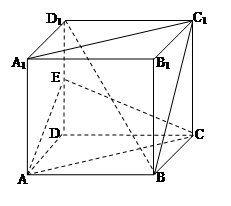
(1)求證: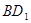 ∥平面AEC;
∥平面AEC;
(2)求 與平面
與平面 所成的角.
所成的角.
(1)證明:見解析;(2)直線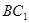 與平面
與平面 所成的角為
所成的角為 .
.
解析試題分析: (1)作AC的中點F,連接EF,則根據三角形的中位線證明線線平行,進而得到線面平行的證明。
(2)要利用線面垂直為前提得到斜線的射影,進而得到線面角的大小。
解:(1)證明:連結BD,交AC于點O,連結EO.
因為E、O分別是 與
與 的中點,
的中點,
所以OE∥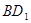 .
.
又因為OE在平面AEC內,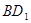 不在平面AEC內,
不在平面AEC內,
所以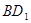 ∥平面AEC.
∥平面AEC.
(2)因為正方體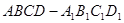 中,
中, ⊥平面ABCD,所以
⊥平面ABCD,所以 ⊥BD,
⊥BD,
又正方形ABCD中,AC⊥BD,
所以BD⊥平面 ,
,
所以∠ 是
是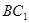 與平面
與平面 所成的角.
所成的角.
設正方體棱長為a, 中,
中, ,
,
所以 ,所以
,所以 ,
,
所以直線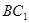 與平面
與平面 所成的角為
所成的角為 .
.
考點:本題主要考查了考查證明線面平行、線面垂直的方法,直線和平面平行的判定,面面垂直的判定,體現了數形結合的數學思想。
點評:解決該試題的關鍵是熟練運用線面平行的判定定理和線面垂直的性質定理得到線面角的大小,進而求解到。


科目:高中數學 來源: 題型:解答題
(本題滿分10分) 在長方體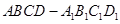 中,
中,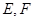 分別是
分別是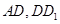 的中點,
的中點,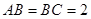 ,
,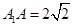 .
.
(Ⅰ)求證: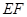 //平面
//平面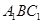 ;
;
(Ⅱ)在線段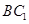 上是否存在點
上是否存在點 ,使直線
,使直線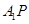 與
與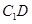 垂直,
垂直,
如果存在,求線段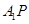 的長,如果不存在,請說明理由.
的長,如果不存在,請說明理由.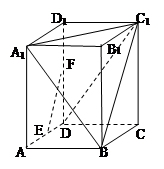
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)如圖,在四棱錐 中,底面
中,底面 是正方形,側棱
是正方形,側棱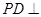 底面
底面 ,
,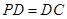 ,
,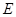 是
是 的中點,作
的中點,作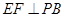 交
交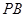 于點
于點 .
.
(1)證明 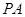 //平面
//平面 ;
;
(2)求二面角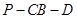 的大小;
的大小;
(3)證明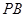 ⊥平面
⊥平面 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知梯形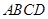 中,
中, ∥
∥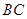 ,
,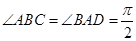 ,
,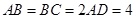 ,
,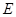 、
、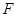 分別是
分別是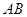 、
、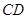 上的點,
上的點,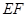 ∥
∥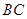 ,
,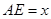 ,
,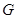 是
是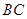 的中點.沿
的中點.沿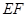 將梯形
將梯形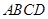 翻折,使平面
翻折,使平面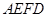 ⊥平面
⊥平面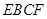 (如圖).
(如圖).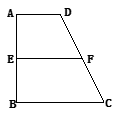
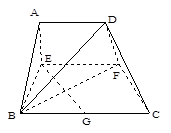
(I)當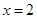 時,求證:
時,求證: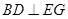 ;
;
(II)若以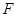 、
、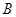 、
、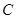 、
、 為頂點的三棱錐的體積記為
為頂點的三棱錐的體積記為 ,求
,求 的最大值;
的最大值;
(III)當 取得最大值時,求二面角
取得最大值時,求二面角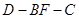 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com