
【題目】如圖,已知雙曲線![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,過右焦點作平行于一條漸近線的直線交雙曲線于點
,過右焦點作平行于一條漸近線的直線交雙曲線于點![]() ,若
,若![]() 的內(nèi)切圓半徑為
的內(nèi)切圓半徑為![]() ,則雙曲線的離心率為( )
,則雙曲線的離心率為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
設(shè)雙曲線的左、右焦點分別為![]() ,
,![]() ,設(shè)雙曲線的一條漸近線方程為
,設(shè)雙曲線的一條漸近線方程為![]() ,可得直線
,可得直線![]() 的方程為
的方程為![]() ,聯(lián)立雙曲線的方程可得
,聯(lián)立雙曲線的方程可得![]() 的坐標(biāo),設(shè)
的坐標(biāo),設(shè)![]() ,
,![]() ,運用三角形的等積法,以及雙曲線的定義,結(jié)合銳角三角函數(shù)的定義,化簡變形可得
,運用三角形的等積法,以及雙曲線的定義,結(jié)合銳角三角函數(shù)的定義,化簡變形可得![]() ,
,![]() 的方程,結(jié)合離心率公式可得所求值.
的方程,結(jié)合離心率公式可得所求值.
設(shè)雙曲線的左、右焦點分別為![]() ,
,![]() ,
,
設(shè)雙曲線的一條漸近線方程為![]() ,
,
可得直線![]() 的方程為
的方程為![]() ,與雙曲線
,與雙曲線![]() 聯(lián)立,
聯(lián)立,
可得![]() ,
,![]() ,
,
設(shè)![]() ,
,![]() ,
,
由三角形的面積的等積法可得![]() ,
,
化簡可得![]() ①
①
由雙曲線的定義可得![]() ②
②
在三角形![]() 中
中![]() ,
,![]() 為直線
為直線![]() 的傾斜角),
的傾斜角),
由![]() ,
,![]() ,可得
,可得![]() ,
,
可得![]() ,③
,③
由①②③化簡可得![]() ,
,
即為![]() ,
,
可得![]() ,則
,則![]() .
.
故選:C.


 學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案 浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案 小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案
小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業(yè)江西人民出版社系列答案
波波熊暑假作業(yè)江西人民出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲乙兩人進(jìn)行乒乓球比賽,兩人打到![]() 平,之后的比賽要每球交替發(fā)球權(quán)且要一人凈勝兩球才能取勝,已知甲發(fā)球甲獲勝的概率為
平,之后的比賽要每球交替發(fā)球權(quán)且要一人凈勝兩球才能取勝,已知甲發(fā)球甲獲勝的概率為![]() ,乙發(fā)球甲獲勝的概率為
,乙發(fā)球甲獲勝的概率為![]() ,則下列命題正確的個數(shù)為( )
,則下列命題正確的個數(shù)為( )
(1)若![]() ,兩人能在兩球后結(jié)束比賽的概率與
,兩人能在兩球后結(jié)束比賽的概率與![]() 有關(guān)
有關(guān)
(2)若![]() ,兩人能在兩球后結(jié)束比賽的概率與
,兩人能在兩球后結(jié)束比賽的概率與![]() 有關(guān)
有關(guān)
(3)第二球分出勝負(fù)的概率與在第二球沒有分出勝負(fù)的情況下進(jìn)而第四球分出勝負(fù)的概率相同
(4)第二球分出勝負(fù)的概率與在第![]() 球沒有分出勝負(fù)的情況下進(jìn)而第
球沒有分出勝負(fù)的情況下進(jìn)而第![]() 球分出勝負(fù)的概率相同
球分出勝負(fù)的概率相同
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線C:![]() 的焦點為F,直線y=4與y軸的交點為P,與C的交點為Q,且
的焦點為F,直線y=4與y軸的交點為P,與C的交點為Q,且![]() .
.
(1)求拋物線C的方程;
(2)過F的直線l與C相交于A,B兩點,若AB的垂直平分線![]() 與C相交于M,N兩點,且A,M,B,N四點在同一個圓上,求直線l的方程.
與C相交于M,N兩點,且A,M,B,N四點在同一個圓上,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
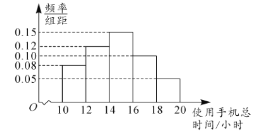
【題目】為了解學(xué)生課外使用手機(jī)的情況,某學(xué)校收集了本校500名學(xué)生2019年12月課余使用手機(jī)的總時間(單位:小時)的情況.從中隨機(jī)抽取了50名學(xué)生,將數(shù)據(jù)進(jìn)行整理,得到如圖所示的頻率分布直方圖.已知這50名學(xué)生中,恰有3名女生課余使用手機(jī)的總時間在![]() ,現(xiàn)在從課余使用手機(jī)總時間在
,現(xiàn)在從課余使用手機(jī)總時間在![]() 的樣本對應(yīng)的學(xué)生中隨機(jī)抽取3名,則至少抽到2名女生的概率為( )
的樣本對應(yīng)的學(xué)生中隨機(jī)抽取3名,則至少抽到2名女生的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體ABCD-ABCD中,平面![]() 垂直于對角線AC,且平面
垂直于對角線AC,且平面![]() 截得正方體的六個表面得到截面六邊形,記此截面六邊形的面積為S,周長為l,則( )
截得正方體的六個表面得到截面六邊形,記此截面六邊形的面積為S,周長為l,則( )
A. S為定值,l不為定值 B. S不為定值,l為定值
C. S與l均為定值 D. S與l均不為定值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,a為常數(shù).
,a為常數(shù).
(1)討論函數(shù)![]() 的單調(diào)性:
的單調(diào)性:
(2)若函數(shù)![]() 有兩個極值點
有兩個極值點![]() ,
,![]() 且
且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】維生素C又叫抗壞血酸,是一種水溶性維生素,是高等靈長類動物與其他少數(shù)生物的必需營養(yǎng)素.維生素C雖不直接構(gòu)成腦組織,也不向腦提供活動能源,但維生素C有多種健腦強(qiáng)身的功效,它是腦功能極為重要的營養(yǎng)物.維生素C的毒性很小,但食用過多仍可產(chǎn)生一些不良反應(yīng).根據(jù)食物中維C的含量可大致分為:含量很豐富:鮮棗、沙棘、獼猴桃、柚子,每100克中的維生素C含量超過100毫克;比較豐富:青椒、桂圓、番茄、草莓、甘藍(lán)、黃瓜、柑橘、菜花,每100克中維生素C含量超過50毫克;相對豐富:白菜、油菜、香菜、菠菜、芹菜、莧菜、菜苔、豌豆、豇豆、蘿卜,每100克中維生素C含量超過30~50毫克.現(xiàn)從獼猴桃、柚子兩種食物中測得每100克所含維生素C的量(單位:![]() )得到莖葉圖如圖所示,則下列說法中不正確的是( )
)得到莖葉圖如圖所示,則下列說法中不正確的是( )
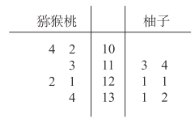
A.獼猴桃的平均數(shù)小于柚子的平均數(shù)
B.獼猴桃的方差小于柚子的方差
C.獼猴桃的極差為32
D.柚子的中位數(shù)為121
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四棱錐![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,
,![]() ,三角形
,三角形![]() 是邊長為2的正三角形,當(dāng)四棱錐
是邊長為2的正三角形,當(dāng)四棱錐![]() 的外接球的體積取得最小值時,則以下判斷正確的是( )
的外接球的體積取得最小值時,則以下判斷正確的是( )
A.四棱錐![]() 的體積取得最小值為
的體積取得最小值為![]() ,外接球的球心必在四棱錐
,外接球的球心必在四棱錐![]() 內(nèi)
內(nèi)
B.四棱錐![]() 的體積取得最小值為
的體積取得最小值為![]() ,外接球的球心可在四棱錐
,外接球的球心可在四棱錐![]() 內(nèi)或外
內(nèi)或外
C.四棱錐![]() 的體積為
的體積為![]() ,外接球的球心必在四棱錐
,外接球的球心必在四棱錐![]() 內(nèi)
內(nèi)
D.四棱錐![]() 的體積為
的體積為![]() ,外接球的球心可在四棱錐
,外接球的球心可在四棱錐![]() 內(nèi)或外
內(nèi)或外
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù),且
為參數(shù),且![]() ),以坐標(biāo)原點
),以坐標(biāo)原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,直線
軸的正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出曲線![]() 和直線
和直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若直線![]() 與
與![]() 軸交點記為
軸交點記為![]() ,與曲線
,與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com