
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 9 |
| 160 |
| 1 |
| 13 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(07年上海卷理)(18分)
若有窮數列![]() (
(![]() 是正整數),滿足
是正整數),滿足![]() 即
即![]() (
(![]() 是正整數,且
是正整數,且![]() ),就稱該數列為“對稱數列”。
),就稱該數列為“對稱數列”。
(1)已知數列![]() 是項數為7的對稱數列,且
是項數為7的對稱數列,且![]() 成等差數列,
成等差數列,![]() ,試寫出
,試寫出![]() 的每一項
的每一項
(2)已知![]() 是項數為
是項數為![]() 的對稱數列,且
的對稱數列,且![]() 構成首項為50,公差為
構成首項為50,公差為![]() 的等差數列,數列
的等差數列,數列![]() 的前
的前![]() 項和為
項和為![]() ,則當
,則當![]() 為何值時,
為何值時,![]() 取到最大值?最大值為多少?
取到最大值?最大值為多少?
(3)對于給定的正整數![]() ,試寫出所有項數不超過
,試寫出所有項數不超過![]() 的對稱數列,使得
的對稱數列,使得![]() 成為數列中的連續項;當
成為數列中的連續項;當![]() 時,試求其中一個數列的前2008項和
時,試求其中一個數列的前2008項和![]()
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西省高三4月月考數學文理合卷試卷(解析版) 題型:解答題
已知各項均不相等的等差數列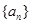 的前三項和為18,
的前三項和為18,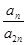 是一個與
是一個與 無關的常數,若
無關的常數,若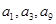 恰為等比數列
恰為等比數列 的前三項,(1)求
的前三項,(1)求 的通項公式.(2)記數列
的通項公式.(2)記數列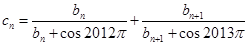 ,
, 的前三
的前三 項和為
項和為 ,求證:
,求證: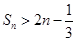
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com