
 的取值范圍是 .
的取值范圍是 . 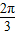 ,進而求出cos2A+cos2B=
,進而求出cos2A+cos2B= cos(2A+
cos(2A+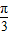 )+1,根據余弦函數的性質得出答案.
)+1,根據余弦函數的性質得出答案. (2cos2A-1)+
(2cos2A-1)+ +
+ (2cos2B-1)+
(2cos2B-1)+
 cos2A+
cos2A+ cos2B+1
cos2B+1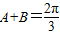
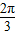 -A
-A cos2A+
cos2A+ cos2B+1
cos2B+1 cos2A+
cos2A+ cos(
cos(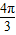 -2A)+1
-2A)+1 cos2A+
cos2A+ [(-
[(- cos2A)-
cos2A)-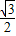 sin2A]+1
sin2A]+1 (
( cos2A-
cos2A-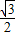 sin2A)+1
sin2A)+1 cos(2A+
cos(2A+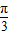 )+1
)+1 cos(2A+
cos(2A+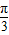 )+1
)+1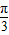 )≤1
)≤1 ≤
≤ cos(2A+
cos(2A+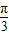 )+1≤
)+1≤
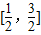
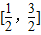


科目:高中數學 來源:2014屆浙江省寧波市高一下學期期中聯考數學試卷(解析版) 題型:選擇題
在 中,點D在線段BC的延長線上,且
中,點D在線段BC的延長線上,且 ,點O在線段CD上(與點C、D不重合),若
,點O在線段CD上(與點C、D不重合),若 的取值范圍是 (
)
的取值范圍是 (
)
A. B.
B. C.
C. D.
D.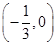
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com