
【題目】如圖,在直三棱柱ABC A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分別是A1C1,BC的中點.

(1)證明:平面AEB⊥平面BB1C1C;
(2)證明:C1F∥平面ABE;
(3)設P是BE的中點,求三棱錐P B1C1F的體積.
【答案】(1) (2)見解析 (3) ![]()
【解析】
(1)證明 在△ABC中,∵AC=2BC=4,∠ACB=60°,由余弦定理得:
∴AB=2![]() ,∴AB2+BC2=AC2,
,∴AB2+BC2=AC2,
∴AB⊥BC,
由已知AB⊥BB1,又BB1∩BC=B,∴AB⊥面BB1C1C,
又∵AB面ABE,∴平面ABE⊥平面BB1C1C.
(2)證明 取AC的中點M,連接C1M,FM
在△ABC,FM∥AB,而FM平面ABE,AB平面ABE,
∴直線FM∥平面ABE
在矩形ACC1A1中,E,M都是中點,∴C1E綉AM,四邊形AMC1B是平面四邊形,∴C1M∥AE
而C1M平面ABE,AE平面ABE,∴直線C1M∥ABE
又∵C1M∩FM=M,∴平面ABE∥平面FMC1,而CF1平面FMC1,
故C1F∥平面AEB.
(3)解 取B1C1的中點H,連接EH,則EH∥A1B1,所以EH∥AB且EH=![]() AB=
AB=![]() ,
,
由(1)得AB⊥面BB1C1C,∴EH⊥面BB1C1C,
∵P是BE的中點,
∴VPB1C1F=![]() VEB1C1F=
VEB1C1F=![]() ×
×![]() S△B1C1F·EH=
S△B1C1F·EH=![]()


科目:高中數學 來源: 題型:
【題目】(2017·南充調研)如圖,在長方體ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一質點從頂點A射向點E(4,3,12),遇長方體的面反射(反射服從光的反射原理),將第i-1次到第i次反射點之間的線段記為Li(i=2,3,4),L1=AE,將線段L1,L2,L3,L4豎立放置在同一水平線上,則大致的圖形是( )
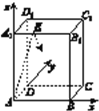
A. 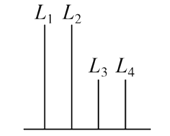 B.
B. 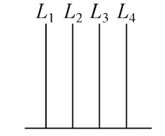
C. 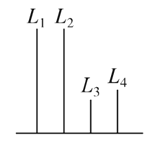 D.
D. 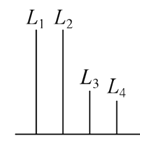
查看答案和解析>>
科目:高中數學 來源: 題型:
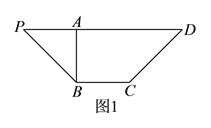
【題目】如圖![]() ,等腰梯形
,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于點
于點![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
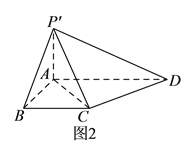
把![]() 折起到
折起到![]() 的位置(如圖
的位置(如圖![]() ),使
),使![]() .
.
(I)求證: ![]() 平面
平面![]() .
.
(II)求三棱錐![]() 的體積.
的體積.
(III)線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ,若存在,指出點
,若存在,指出點![]() 的位置并證明;若不存在,請說明理由.
的位置并證明;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學名著《九章算術》中有這樣一個問題:今有牛、馬、羊食人苗,苗主責之粟五斗,羊主曰:“我羊食半馬.”馬主曰:“我馬食半牛.”今欲衰償之,問各出幾何?此問題的譯文是:今有牛、馬、羊吃了別人的禾苗,禾苗主人要求賠償5斗粟.羊主人說:“我羊所吃的禾苗只有馬的一半.”馬主人說:“我馬所吃的禾苗只有牛的一半.”打算按此比例償還,他們各應償還多少?已知牛、馬、羊的主人各應償還![]() 升,
升, ![]() 升,
升, ![]() 升,1斗為10升,則下列判斷正確的是( )
升,1斗為10升,則下列判斷正確的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比為2的等比數列,且
依次成公比為2的等比數列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比為2的等比數列,且
依次成公比為2的等比數列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比為
依次成公比為![]() 的等比數列,且
的等比數列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比為
依次成公比為![]() 的等比數列,且
的等比數列,且![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明設置的手機開機密碼若連續3次輸入錯誤,則手機被鎖定,5分鐘后,方可重新輸入.
某日,小明忘記了開機密碼,但可以確定正確的密碼是他常用的4個密碼之一,于是,他
決定逐個(不重復)進行嘗試.
(1)求手機被鎖定的概率;
(2)設第![]() 次輸入后能成功開機,求
次輸入后能成功開機,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com