
【題目】已知函數![]() ,若關于x的方程
,若關于x的方程![]() 有四個不等實根,且
有四個不等實根,且![]() 恒成立,則實數
恒成立,則實數![]() 的最小值為________.
的最小值為________.
【答案】![]()
【解析】
函數![]() 是分段函數,通過求導分析得到函數
是分段函數,通過求導分析得到函數![]() 在
在![]() 上為增函數,在
上為增函數,在![]() 上為增函數,在
上為增函數,在![]() 上為減函數,求得函數
上為減函數,求得函數![]() 在
在![]() 上,當
上,當![]() 時有一個極大值1,所以要使方程
時有一個極大值1,所以要使方程![]() 有四個實數根,
有四個實數根,![]() 的值一個要在
的值一個要在![]() 內,一個在
內,一個在![]() 內,然后運用二次函數的圖象及二次方程根的關系列式求解
內,然后運用二次函數的圖象及二次方程根的關系列式求解![]() 和
和![]() 的取值范圍,從而求出
的取值范圍,從而求出![]() 的最小值.
的最小值.
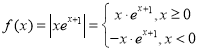 ,
,
當![]() 時,
時,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上為增函數,
上為增函數,
當![]() 時,
時,![]() ,
,
由![]() ,得
,得![]() ,當
,當![]() 時,
時,![]() ,
,![]() 為增函數,
為增函數,
當![]() 時,
時,![]() ,
,![]() 為減函數,
為減函數,
所以函數![]() 的極大值為
的極大值為![]() ,
,
極小值為:![]() ,如圖:
,如圖:
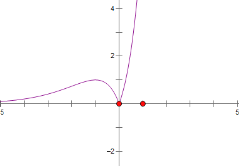
令![]() ,由韋達定理得:
,由韋達定理得:![]() ,
,![]() ,
,
(1)因為當![]() ,且
,且![]() 時,方程
時,方程![]() 沒有實根,故舍去.
沒有實根,故舍去.
(2)又當![]() ,且
,且![]() (不妨設),由圖象可得
(不妨設),由圖象可得![]() 至多有三個實根,
至多有三個實根,
由此可得方程![]() 至多有三個實根,不符合題意.
至多有三個實根,不符合題意.
(3)若![]() 是方程
是方程![]() 的根,代入可得
的根,代入可得![]() ,所以
,所以![]() ,解得
,解得![]() ,而根據圖象可知
,而根據圖象可知![]() 無解,
無解,![]() 和
和![]() 都只有一個根,不符合題意.
都只有一個根,不符合題意.
故要使方程![]() 有四個不等實數根,
有四個不等實數根,
則方程![]() 應有兩個不相同的正實根,
應有兩個不相同的正實根,
即![]() ,且
,且![]() ,此時
,此時![]() ,且一個根在
,且一個根在![]() 內,一個根在
內,一個根在![]() 內,
內,
再令![]() ,
,
因為![]() ,①
,①![]() ,
,
則![]() ,②
,②
則只需![]() ,即
,即![]() ,
,
所以![]() ,③
,③
將③式平方可得:![]() ,④
,④
由①②解得:![]() ,⑤
,⑤
由④得到:![]() ,由④⑤得到:
,由④⑤得到:![]() ,
,
所以![]() ,
,![]() .
.
所以本題答案為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】我市準備實施天然氣價格階梯制,現提前調查市民對天然氣價格階梯制的態度,隨機抽查了![]() 名市民,現將調查情況整理成了被調查者的頻率分布直方圖(如圖)和贊成者的頻數表如下:
名市民,現將調查情況整理成了被調查者的頻率分布直方圖(如圖)和贊成者的頻數表如下:
年齡(歲) |
|
|
|
|
|
|
贊成人數 |
|
|
|
|
|
|
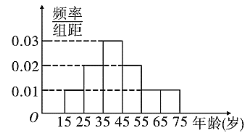
(1)若從年齡在![]() ,
,![]() 的被調查者中各隨機選取
的被調查者中各隨機選取![]() 人進行調查,求所選取的
人進行調查,求所選取的![]() 人中至少有
人中至少有![]() 人對天然氣價格階梯制持贊成態度的概率;
人對天然氣價格階梯制持贊成態度的概率;
(2)若從年齡在![]() ,
,![]() 的被調查者中各隨機選取
的被調查者中各隨機選取![]() 人進行調查,記選取的
人進行調查,記選取的![]() 人中對天然氣價格實施階梯制持不贊成態度的人數為
人中對天然氣價格實施階梯制持不贊成態度的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次田徑比賽中,35名運動員的成績(單位:分鐘)的莖葉圖如圖所示。

若將運動員按成績由好到差編為1—35號,再用系統抽樣方法從中抽取5人,則其中成績在區間![]() 上的運動員人數為
上的運動員人數為
A.6B.5C.4D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖象如圖所示:
的部分圖象如圖所示:

(I)求![]() 的解析式及對稱中心坐標;
的解析式及對稱中心坐標;
(Ⅱ)將![]() 的圖象向右平移
的圖象向右平移![]() 個單位,再將橫坐標伸長到原來的2倍,縱坐標不變,最后將圖象向上平移1個單位,得到函數
個單位,再將橫坐標伸長到原來的2倍,縱坐標不變,最后將圖象向上平移1個單位,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在
在![]() 上的單調區間及最值.
上的單調區間及最值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中點,E是PB中點.
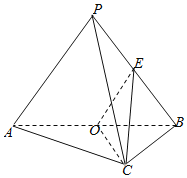
(1)證明:平面PAB⊥平面ABC;
(2)求點B到平面OEC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業有甲、乙兩套設備生產同一種產品,為了檢測兩套設備的生產質量情況,隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本,檢測一項質量指標值,若該項質量指標值落在![]() 內,則為合格品,否則為不合格品.表1是甲套設備的樣本的頻數分布表,圖1是乙套設備的樣本的頻率分布直方圖.
內,則為合格品,否則為不合格品.表1是甲套設備的樣本的頻數分布表,圖1是乙套設備的樣本的頻率分布直方圖.
表1:甲套設備的樣本的頻數分布表
質量指標值 |
|
|
|
|
|
|
頻數 | 1 | 5 | 18 | 19 | 6 | 1 |
圖1:乙套設備的樣本的頻率分布直方圖
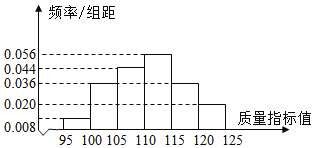
(1)根據表1和圖1,通過計算合格率對兩套設備的優劣進行比較;
(2)填寫下面列聯表,并根據列聯表判斷是否有![]() 的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.
的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.
甲套設備 | 乙套設備 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
附:
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
參考公式: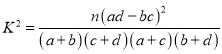 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() 為自然對數的底數).
為自然對數的底數).
(1)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求
垂直,求![]() 的單調區間;
的單調區間;
(2)若函數![]() 有兩個極值點,求實數
有兩個極值點,求實數![]() 的取值范圍;
的取值范圍;
(3)證明:當![]() 時,
時,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com