Question

為了了解已有沙漠面積1000萬公頃的某地區沙漠面積的變化情況，環保監測部門進入了連續4年的觀察，并將每年年底的觀察結果記錄如表甲．根據這些數據還可繪制曲線圖乙．由此預測到該地區沙漠的面積將繼續擴大．

表甲

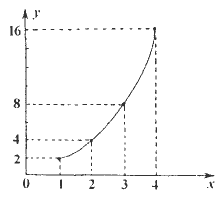
圖乙

(1)如果不采取任何措施，那么到第m年底，該地區沙漠面積變為多少公傾？

(2)如果第5年底后，采取引水和植樹造林等措施，使沙漠化擴大趨勢得以減緩．第6年開始的每一年年底觀察得該地區沙漠面積比上一年增加數y(公頃)分別為：a₆，a₇，a₈，…，a_n，而a₆，a₇，a₈，…，a_n還構成首項a₆＝32，公差d＝－8的遞減等差數列．當沙漠化擴大趨勢停止后(即a_n＝0)，每年改造18萬公頃沙漠，那么第n年底，該地區沙漠的面積能減少到980萬公頃？

Answer 1

答案：
解析：

思路　　本題利用圖表形式說明條件的命題方式，是近年來突出培養學生識圖能力的一種體現．同時還考察了等差、等比數列的基本性質．結合表甲和圖乙，我們可以清楚地看出沙漠逐年增加的面積數a1，a2，a3，a4，構成首項為2，公比為2的等比數列．利用等比數列求和公式不難算出第m年底沙漠的總面積． 　　根據題意，第6年底開始，沙漠面積增加的數量a6，a7，…，an變為遞減的等差數列．而當an＝0時，說明沙漠擴大化趨勢的終止，再以此時沙漠總面積為基數，每年減少18萬公頃，便容易推算出沙漠總面積減少到980萬公頃所需的時間，三段時間相加，便可得到最后答案． 　　解答　　(1)設an表示第n年比前一年沙漠面積的增加數． 　　由表甲和圖乙得：an＝2n(n∈N*)，則第m年底沙漠總面積 　　Sm＝1000＋a1＋a2＋…＋am 　　＝1000＋21＋22＋…＋2m 　　＝1000＋ 　　＝998＋2m+1(萬公頃)； 　　(2)由(1)中結論，可知第5年底的沙漠面積S5＝998＋25+1＝1062，根據題意，改造沙漠后，a6，a7，…，an構成以a6＝32為首項，公差d＝－8的等差數列． 　　則an＝a6＋(n－6)d(n≥6，n∈N*)， 　　即an＝32＋(n－6)·(－8)＝80－8n 　　當an＝0時，解得n＝10． 　　∴當第10年底，沙漠擴大化趨勢終止，此時沙漠總面積為 　　S10＝1062＋＝1142(萬公頃)． 　　再根據條件，從第11年開始，沙漠總面積每年減少18萬公頃，至總面積達到980萬公頃．設再需p年，則有 　　1142－18p＝980．解得p＝9， 　　即10＋9＝19． 　　∴到19年底，該地區沙漠的總面積能減少到980萬公頃．