
(請考生在下面甲、乙兩題中任選一題做答,如果多做,則按所做的甲題計分)
甲題 :
(1)若關于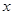 的不等式
的不等式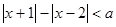 的解集不是空集,求實數
的解集不是空集,求實數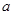 的取值范圍;
的取值范圍;
(2)已知實數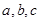 ,滿足
,滿足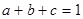 ,求
,求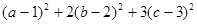 最小值.
最小值.
乙題:
已知曲線C的極坐標方程是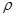 =4cos
=4cos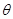 。以極點為平面直角坐標系的原點,極軸為
。以極點為平面直角坐標系的原點,極軸為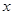 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線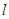 的參數方程是
的參數方程是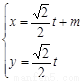 (
(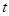 是參數)。
是參數)。
(1)將曲線C的極坐標方程化成直角坐標方程并把直線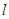 的參數方程轉化為普通方程;
的參數方程轉化為普通方程;
(2) 若過定點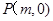 的直線
的直線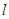 與曲線C相交于A、B兩點,且
與曲線C相交于A、B兩點,且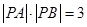 ,試求實數
,試求實數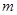 的值。
的值。
甲題:(1)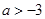
(2)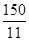
乙題:(1)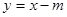
(2)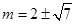 或
或
【解析】甲題:(1)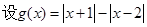 ,
,
由題意得: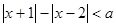 的解集不是空集,即
的解集不是空集,即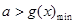 …………2分
…………2分
又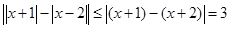 ,所以
,所以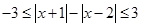
所以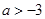 。…………7分
。…………7分
(2)由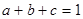 及柯西不等式得
及柯西不等式得
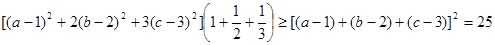 ,…11分
,…11分
所以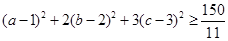 , …12分
, …12分
當且僅當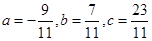 取等號,….14分
取等號,….14分
故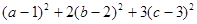 最小值為
最小值為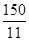 ……15分
……15分
乙題:(1)曲線C的直角坐標方程是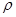 =4cos
=4cos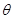 ,化為直角坐標方程為:
,化為直角坐標方程為:
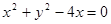 …………4分
…………4分
直線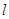 的直角坐標方程為:
的直角坐標方程為: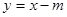 …………7分
…………7分
(2)由直線參數方程的幾何意義將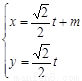
代入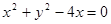 得:
得: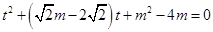 , (*)…………9分
, (*)…………9分
記兩個根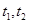 , 所以
, 所以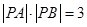 得
得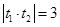 ,…………10分
,…………10分
由韋達定理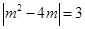 ,
,
當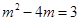 時,解得:
時,解得: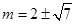 …………12分
…………12分
當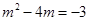 時,解得:
時,解得: …………14分
…………14分
經檢驗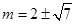 或
或 時(*)
時(*)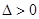 均符合題意。…………15分
均符合題意。…………15分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:浙江省寧波市09-10學年高二期末八校聯考數學試卷(文科) 題型:解答題
(請考生在下面甲、乙兩題中任選一題做答,如果多做,則按所做的甲題計分)
甲題 :
⑴ 若關于 的不等式
的不等式 的解集不是空集,求實數
的解集不是空集,求實數 的取值范圍;
的取值范圍;
⑵
已知實數 ,滿足
,滿足 ,求
,求 最小值.
最小值.
乙題:
已知曲線C的極坐標方程是 =4cos
=4cos 。以極點為平面直角坐標系的原點,極軸為
。以極點為平面直角坐標系的原點,極軸為 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線 的參數方程是
的參數方程是 (
( 是參數)。
是參數)。
⑴ 將曲線C的極坐標方程化成直角坐標方程并把直線 的參數方程轉化為普通方程;
的參數方程轉化為普通方程;
⑵ 若過定點 的直線
的直線 與曲線C相交于A、B兩點,且
與曲線C相交于A、B兩點,且 ,試求實數
,試求實數 的值。
的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com