（）（本小題滿分12分）
設函數(shù)
,其中常數(shù)
(Ⅰ)討論
的單調(diào)性;
(Ⅱ)若當x≥0時，>0恒成立，求
的取值范圍.
：（I）
由
知，當
時，
，故
在區(qū)間
是增函數(shù)；
當
時，
，故在區(qū)間
是減函數(shù)；
當
時，，故在區(qū)間
是增函數(shù).
綜上，當時，在區(qū)間和是增函數(shù)，在區(qū)間是減函數(shù).
（II）由（I）知，當
時，在
或
處取得最小值.
由假設知
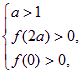即
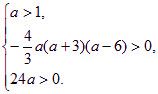解得 
故
的取值范圍是（1，6）w.w.w.k.s.5.u.c.o.m 
：因為第(Ⅰ)題中要求函數(shù)的單調(diào)區(qū)間,利用導數(shù)的正負即可求出,所以首先要求出函數(shù)的導數(shù),然后解不等式和即可. 第(Ⅱ)小題是一個恒成立問題,轉(zhuǎn)化為求函數(shù)的最值解決,所以要求出函數(shù)在x≥0時的最小值.
數(shù)學奧賽暑假天天練南京大學出版社系列答案科目：高中數(shù)學 來源： 題型：
| 3 |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
（本小題滿分12分）已知關(guān)于
的一元二次函數(shù)
（Ⅰ）設集合P={1，2， 3}和Q={－1，1，2，3，4}，分別從集合P和Q中隨機取一個數(shù)作為
和
，求函數(shù)
在區(qū)間[
上是增函數(shù)的概率；（Ⅱ）設點（，）是區(qū)域
內(nèi)的隨機點，求函數(shù)
上是增函數(shù)的概率。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
(本小題滿分12分) 一幾何體
的三視圖如圖所示，
,A1A=
,AB=
,AC=2,A1C1=1,
在線段
上且
=
.
(I)證明:平面
⊥平面
；
(II)求二面角
的余弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，且
。①求
的最大值及最小值；②求