已知命題
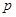
:方程
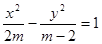
表示焦點在
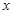
軸上的雙曲線。命題
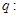
曲線
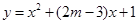
與
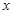
軸交于不同的兩點,若
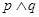
為假命題,
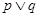
為真命題,求實數(shù)
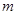
的取值范圍。
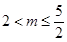
或
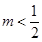
.
試題分析:分別求出命題p、q為真命題時m的范圍,根據(jù)復合命題真值表可得命題p,q命題一真一假,分p真q假和p假q真求出m的范圍,再求并集.
試題解析:若
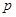
真得:
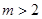
2分;
若
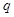
真得:
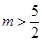
或
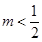
4分;
∵
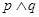
為假命題,
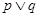
也為真命題
∴
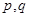
命題一真一假 6分;
若
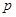
真
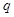
假:
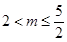
; 8分;
若
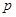
假
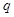
真:
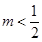
10分
∴實數(shù)
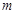
的取值范圍為:
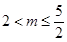
或
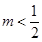
12分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知中心在原點的雙曲線C的一個焦點是F
1(一3,0),一條漸近線的方程是
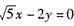
(1)求雙曲線C的方程;
(2)若以k(k≠0)為斜率的直線
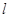
與雙曲線C相交于兩個不同的點M, N,且線段MN的
垂直平分線與兩坐標軸圍成的三角形的面積為
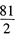
,求k的取值范圍。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線
C∶
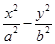
=1(
a>0,
b>0)的實軸長為2,離心率為2,則雙曲線
C的焦點坐標是________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知雙曲線
C與橢圓
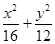
=1有共同的焦點
F1,
F2,且離心率互為倒數(shù).若雙曲線右支上一點
P到右焦點
F2的距離為4,則
PF2的中點
M到坐標原點
O的距離等于( ).
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線
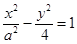
的右焦點與拋物線y
2=12x的焦點重合,則該雙曲線的焦點到其漸近線的距離等于
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
雙曲線
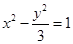
的左右兩支上各有一點
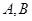
,點
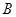
在直線
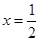
上的射影是點
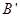
,若直線
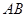
過右焦點,則直線
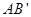
必過點( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
雙曲線
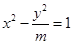
的離心率大于
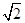
的充分必要條件是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設雙曲線
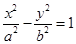
的兩條漸近線與直線
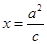
分別交于
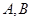
兩點,
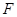
為該雙曲線的右焦點.若
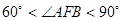
, 則該雙曲線的離心率的取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線

=1(
a>0,
b>0)的漸近線方程為
y=±
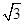 x
x,則它的離心率為________.
查看答案和解析>>

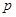 :方程
:方程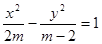 表示焦點在
表示焦點在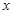 軸上的雙曲線。命題
軸上的雙曲線。命題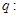 曲線
曲線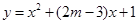 與
與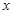 軸交于不同的兩點,若
軸交于不同的兩點,若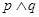 為假命題,
為假命題,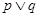 為真命題,求實數(shù)
為真命題,求實數(shù)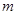 的取值范圍。
的取值范圍。 閱讀快車系列答案
閱讀快車系列答案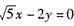
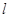 與雙曲線C相交于兩個不同的點M, N,且線段MN的
與雙曲線C相交于兩個不同的點M, N,且線段MN的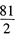 ,求k的取值范圍。
,求k的取值范圍。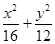 =1有共同的焦點F1,F2,且離心率互為倒數(shù).若雙曲線右支上一點P到右焦點F2的距離為4,則PF2的中點M到坐標原點O的距離等于( ).
=1有共同的焦點F1,F2,且離心率互為倒數(shù).若雙曲線右支上一點P到右焦點F2的距離為4,則PF2的中點M到坐標原點O的距離等于( ).