
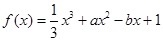 (
(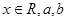 為實數)有極值,且在
為實數)有極值,且在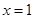 處的切線與直線
處的切線與直線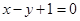 平行.
平行.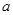 的取值范圍;
的取值范圍;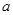 ,使得函數
,使得函數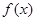 的極小值為1,若存在,求出實數
的極小值為1,若存在,求出實數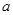 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;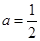 ,
,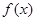 的導數為
的導數為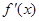 ,令
,令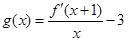
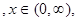
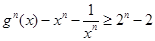
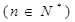
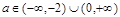 ;
;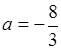 ,使得函數f(x)的極小值為1 ;
,使得函數f(x)的極小值為1 ;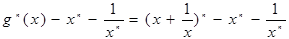
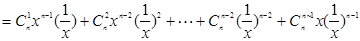
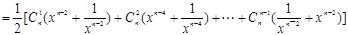
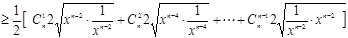
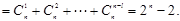
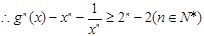
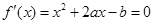 有兩個不同的實數根,從而得到b,a的一個不等式,再根據
有兩個不同的實數根,從而得到b,a的一個不等式,再根據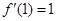 得到a,b的等式,消去b,可以解出a的取值范圍.
得到a,b的等式,消去b,可以解出a的取值范圍.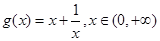 ,然后問題的關鍵是
,然后問題的關鍵是 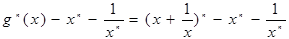
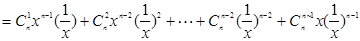
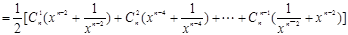
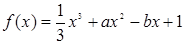 ,∴
,∴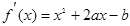 ,由題意∴f/(1)=1+2a-b=1,
,由題意∴f/(1)=1+2a-b=1,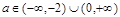 4分
4分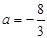 .……………5分
.……………5分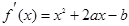 ,令f/(x)=0
,令f/(x)=0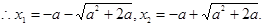

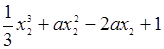 =1,
=1,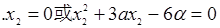 ……………………………………………………7分
……………………………………………………7分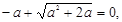 則a=0(舍).……………………8分
則a=0(舍).……………………8分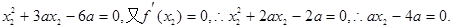
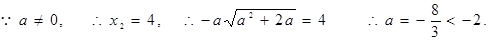
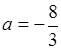 ,使得函數f(x)的極小值為1 ………9分
,使得函數f(x)的極小值為1 ………9分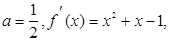
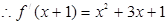 ,
, 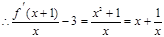
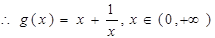 …….l0分
…….l0分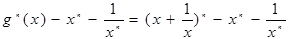
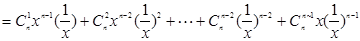
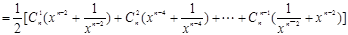
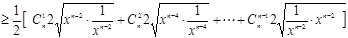
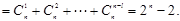
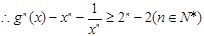 …………………………………………14分
…………………………………………14分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com