
已知各項均為正數的等比數列{an}的公比為q,且0<q<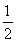 .
.
(1)在數列{an}中是否存在三項,使其成等差數列?說明理由;
(2)若a1=1,且對任意正整數k,ak-(ak+1+ak+2)仍是該數列中的某一項.
(ⅰ)求公比q;
(ⅱ)若bn=-logan+1(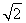 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,試用S2011表示T2011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,試用S2011表示T2011.
(1)不可能(2)(ⅰ)q=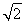 -1(ⅱ)T2011=2012S2011-2011
-1(ⅱ)T2011=2012S2011-2011
【解析】(1)由條件知an=a1qn-1,0<q<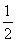 ,a1>0,所以數列{an}是遞減數列.若有ak,am,an(k<m<n)成等差數列,則中項不可能是ak(最大),也不可能是an(最小),
,a1>0,所以數列{an}是遞減數列.若有ak,am,an(k<m<n)成等差數列,則中項不可能是ak(最大),也不可能是an(最小),
若2am=ak+an?2qm-k=1+qn-k,(*)
由2qm-k≤2q<1,1+qh-k>1,知(*)式不成立,
故ak,am,an不可能成等差數列.
(2)(ⅰ)(解法1)ak-ak+1-ak+2=a1qk-1(1-q-q2)=a1qk-1 ,
,
由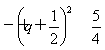 ∈
∈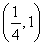 ,知ak-ak+1-ak+2<ak<ak-1<…,
,知ak-ak+1-ak+2<ak<ak-1<…,
且ak-ak+1-ak+2>ak+2>ak+3>…,
所以ak-ak+1-ak+2=ak+1,即q2+2q-1=0,
所以q=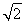 -1.
-1.
(解法2)設ak-ak+1-ak+2=am,則1-q-q2=qm-k,
由1-q-q2∈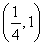 知m-k=1,即m=k+1,
知m-k=1,即m=k+1,
以下同解法1.
(ⅱ)bn=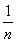 ,
,
(解法1)Sn=1+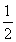 +
+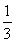 +…+
+…+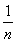 ,
,
Tn=1+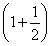 +
+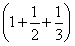 +…+
+…+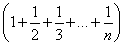
=n+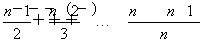 =n
=n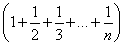 -
-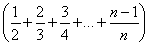
=nSn-[(1-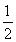 )+(1-
)+(1-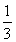 )+(1-
)+(1-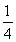 )+…+(1-
)+…+(1-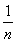 )]
)]
=nSn-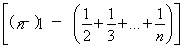 =nSn-
=nSn-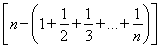
=nSn-n+Sn=(n+1)Sn-n,所以T2011=2012S2011-2011.
(解法2)Sn+1=1+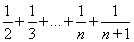 =Sn+
=Sn+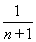 ,所以(n+1)Sn+1-(n+1)Sn=1,
,所以(n+1)Sn+1-(n+1)Sn=1,
所以(n+1)Sn+1-nSn=Sn+1,2S2-S1=S1+1,3S3-2S2=S2+1,……
(n+1)Sn+1-nSn=Sn+1,累加得(n+1)Sn+1-S1=Tn+n,
所以Tn=(n+1)Sn+1-1-n=(n+1)Sn-n=(n+1)(Sn+bn)-1-n
=(n+1)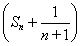 -1-n=(n+1)Sn-n,
-1-n=(n+1)Sn-n,
所以T2011=2012S2011-2011


科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第八章第3課時練習卷(解析版) 題型:解答題
已知如圖①所示,矩形紙片AA′A1′A1,點B、C、B1、C1分別為AA′、A1A1′的三等分點,將矩形紙片沿BB1、CC1折成如圖②形狀(正三棱柱),若面對角線AB1⊥BC1,求證:A1C⊥AB1.
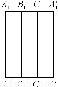
(圖①)
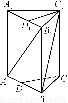
(圖②)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第八章第1課時練習卷(解析版) 題型:填空題
已知點P、Q,平面α,將命題“P∈α,Q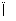 α
α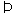 PQ
PQ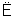 α”改成文字敘述是________.
α”改成文字敘述是________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第6課時練習卷(解析版) 題型:填空題
已知等差數列{an}的前n項和為Sn,若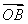 =a100·
=a100·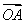 +a101
+a101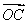 ,且A、B、C三點共線(該直線不過點O),則S200=________.
,且A、B、C三點共線(該直線不過點O),則S200=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第5課時練習卷(解析版) 題型:解答題
設{an}是公比不為1的等比數列,其前n項和為Sn,且a5,a3,a4成等差數列.
(1)求數列{an}的公比;
(2)證明:對任意k∈N+,Sk+2,Sk,Sk+1成等差數列.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第4課時練習卷(解析版) 題型:解答題
已知等差數列{an}是遞增數列,且滿足a4·a7=15,a3+a8=8.
(1)求數列{an}的通項公式;
(2)令bn=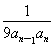 (n≥2),b1=
(n≥2),b1=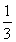 ,求數列{bn}的前n項和Sn.
,求數列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第4課時練習卷(解析版) 題型:填空題
一個等差數列前4項之和為26,最末4項之和為110,所有項之和為187,則它的項數為________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第3課時練習卷(解析版) 題型:填空題
若數列{an}的前n項和為Sn=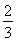 an+
an+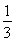 ,則數列{an}的通項公式是an=________.
,則數列{an}的通項公式是an=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第1課時練習卷(解析版) 題型:填空題
設a>0,若an= 且數列{an}是遞增數列,則實數a的范圍是__________.
且數列{an}是遞增數列,則實數a的范圍是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com