Question

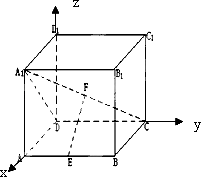
【題目】在邊長是2的正方體ABCD﹣A1B1C1D1中，E，F分別為AB，A1C的中點．應用空間向量方法求解下列問題．

（1）求EF的長
（2）證明：EF∥平面AA1D1D；
（3）證明：EF⊥平面A1CD．

Answer 1

【答案】
（1）解：如圖建立空間直角坐標系，則A1（2，0，2），A（2，0，0），B（2，2，0），C（0，2，0），D1（0，0，2），D（0，0，0），

∵E，F分別為AB，A1C的中點，∴E（2，1，0），F（1，1，1）， =（﹣1，0，1），

∴| |= =

（2）證明：∵ =（﹣2，0，2）=2 ，∴EF∥AD1，

又AD1平面AA1D1D，EF平面AA1D1D，

∴EF∥平面AA1D1D

（3）證明： =（0，﹣2，0）， =（﹣2，0，﹣2），

∵ =0， =0，∴EF⊥CD，EF⊥A1D，又CD∩A1D=D，

∴EF⊥平面A1CD

【解析】（1）建立適當的空間直角坐標系，求出向量 的坐標表示，代入長度公式求解；（2）求出 的坐標表示，關鍵坐標關系判斷EF∥AD1 ， 再利用線面平行的判定定理證明；（3）利用 =0， =0，可證直線EF垂直于CD、A1D，再利用線面垂直的判定定理證明．
【考點精析】根據題目的已知條件，利用直線與平面平行的判定和直線與平面垂直的判定的相關知識可以得到問題的答案，需要掌握平面外一條直線與此平面內的一條直線平行，則該直線與此平面平行；簡記為：線線平行，則線面平行；一條直線與一個平面內的兩條相交直線都垂直，則該直線與此平面垂直；注意點：a)定理中的“兩條相交直線”這一條件不可忽視；b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想．