
(本小題共14分)
已知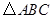 的頂點(diǎn)
的頂點(diǎn) 在橢圓
在橢圓 上,
上, 在直線
在直線 上,且
上,且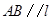 。
。
(Ⅰ)當(dāng) 邊通過坐標(biāo)原點(diǎn)
邊通過坐標(biāo)原點(diǎn)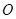 時,求
時,求 的長及
的長及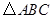 的面積;
的面積;
(Ⅱ)當(dāng)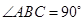 ,且斜邊
,且斜邊 的長最大時,求
的長最大時,求 所在直線的方程。
所在直線的方程。
(Ⅰ)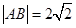 ,
, 。
。
(Ⅱ)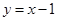
【解析】(Ⅰ)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012051811203634372172/SYS201205181121324531902993_DA.files/image004.png">,且 邊通過點(diǎn)
邊通過點(diǎn)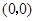 ,所以
,所以 所在直線的方程為
所在直線的方程為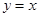 。
。
設(shè)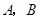 兩點(diǎn)坐標(biāo)分別為
兩點(diǎn)坐標(biāo)分別為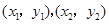 。
。
由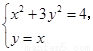 得
得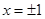 。
。
所以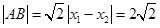 。
。
又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012051811203634372172/SYS201205181121324531902993_DA.files/image005.png">邊上的高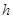 等于原點(diǎn)到直線
等于原點(diǎn)到直線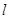 的距離。
的距離。
所以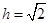 ,
,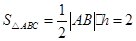 。
。
(Ⅱ)設(shè) 所在直線的方程為
所在直線的方程為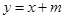 ,
,
由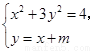 得
得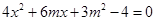 。
。
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012051811203634372172/SYS201205181121324531902993_DA.files/image008.png">在橢圓上,
所以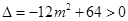 。
。
設(shè) 兩點(diǎn)坐標(biāo)分別為
兩點(diǎn)坐標(biāo)分別為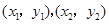 ,
,
則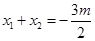 ,
,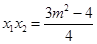 ,
,
所以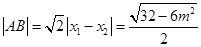 。
。
又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012051811203634372172/SYS201205181121324531902993_DA.files/image024.png">的長等于點(diǎn)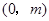 到直線
到直線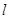 的距離,即
的距離,即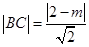 。
。
所以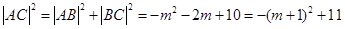 。
。
所以當(dāng)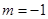 時,
時,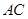 邊最長,(這時
邊最長,(這時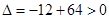 )
)
此時 所在直線的方程為
所在直線的方程為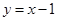 。
。


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(本小題共14分)
數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,點(diǎn)
,點(diǎn)![]() 在直線
在直線![]()
上.
(I)求證:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(II)若數(shù)列![]() 滿足
滿足![]() ,求數(shù)列
,求數(shù)列![]() 的前n項(xiàng)和
的前n項(xiàng)和![]()
(III)設(shè)![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題共14分)
如圖,四棱錐![]() 的底面是正方形,
的底面是正方形,![]() ,點(diǎn)E在棱PB上。
,點(diǎn)E在棱PB上。

(Ⅰ)求證:平面![]() ;
;
(Ⅱ)當(dāng)![]() 且E為PB的中點(diǎn)時,求AE與平面PDB所成的角的大小。
且E為PB的中點(diǎn)時,求AE與平面PDB所成的角的大小。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(2009北京理)(本小題共14分)
已知雙曲線![]() 的離心率為
的離心率為![]() ,右準(zhǔn)線方程為
,右準(zhǔn)線方程為![]()
(Ⅰ)求雙曲線![]() 的方程;
的方程;
(Ⅱ)設(shè)直線![]() 是圓
是圓![]() 上動點(diǎn)
上動點(diǎn)![]() 處的切線,
處的切線,![]() 與雙曲線
與雙曲線![]() 交
交
于不同的兩點(diǎn)![]() ,證明
,證明![]() 的大小為定值.
的大小為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆度廣東省高二上學(xué)期11月月考理科數(shù)學(xué)試卷 題型:解答題
(本小題共14分)在四棱錐P-ABCD中,底面ABCD是正方形,側(cè)棱PD 底面ABCD,PD=DC,點(diǎn)E是PC的中點(diǎn),作EF
底面ABCD,PD=DC,點(diǎn)E是PC的中點(diǎn),作EF PB交PB于點(diǎn)F
PB交PB于點(diǎn)F
⑴求證:PA//平面EDB
⑵求證:PB 平面EFD
平面EFD
⑶求二面角C-PB-D的大小

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年北京市崇文區(qū)高三下學(xué)期二模數(shù)學(xué)(文)試題 題型:解答題
(本小題共14分)
正方體 的棱長為
的棱長為 ,
, 是
是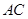 與
與 的交點(diǎn),
的交點(diǎn), 為
為 的中點(diǎn).
的中點(diǎn).
(Ⅰ)求證:直線 ∥平面
∥平面 ;
;
(Ⅱ)求證: 平面
平面 ;
;
(Ⅲ)求三棱錐 的體積.
的體積.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com