
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)設函數![]() ,
, ![]() ,
, ![]() 為自然對數的底數.當
為自然對數的底數.當![]() 時,若
時,若![]() ,
, ![]() ,不等式
,不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
【答案】(1)單調遞減區間是![]() ,單調遞增區間是
,單調遞增區間是![]() ;(2)3
;(2)3
【解析】試題分析:(1)求出函數的導數,解關于導函數的不等式,求出函數的單調區間即可;
(2)問題等價于等價于, ![]() 對
對![]() 恒成立,,設
恒成立,,設![]() ,求出函數的導數,根據函數的單調性求出k的最大值即可.
,求出函數的導數,根據函數的單調性求出k的最大值即可.
試題解析:(1)對函數求導得![]() ,
,
令![]() ,得
,得![]() ,
,
當![]() 時,
時, ![]() ,此時函數
,此時函數![]() 單調遞減;
單調遞減;
當![]() 時,
時, ![]() ,此時函數
,此時函數![]() 單調遞增,
單調遞增,
所以函數![]() 的單調遞減區間是
的單調遞減區間是![]() ,單調遞增區間是
,單調遞增區間是![]() .
.
(2)當![]() 時,由(1)可知
時,由(1)可知![]() ,
,
![]() ,
, ![]() ,不等式
,不等式![]() 成立等價于當
成立等價于當![]() 時,
時, ![]() 恒成立,
恒成立,
即![]() 對
對![]() 恒成立,
恒成立,
因為![]() 時
時![]() ,
,
所以![]() 對
對![]() 恒成立,
恒成立,
即![]() 對
對![]() 恒成立,
恒成立,
設![]() ,
,
則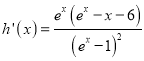 ,
,
令![]() ,則
,則![]() ,
,
當![]() 時,
時, ![]() ,
,
所以函數![]() 在
在![]() 上單調遞增,
上單調遞增,
而![]() ,
, ![]() ,
,
所以![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,即
,即![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() ,所以函數
,所以函數![]() 單調遞減;
單調遞減;
當![]() 時,
時, ![]() ,
, ![]() ,所以函數
,所以函數![]() 單調遞增,
單調遞增,
所以當![]() 時,函數
時,函數![]() 有極小值
有極小值![]() ,同時也為最小值,
,同時也為最小值,
因為![]()
![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 的最大整數值是
的最大整數值是![]() .
.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:
【題目】下圖是某省從1月21日至2月24日的新冠肺炎每日新增確診病例變化曲線圖.

若該省從1月21日至2月24日的新冠肺炎每日新增確診人數按日期順序排列構成數列![]() ,
,![]() 的前n項和為
的前n項和為![]() ,則下列說法中正確的是( )
,則下列說法中正確的是( )
A.數列![]() 是遞增數列B.數列
是遞增數列B.數列![]() 是遞增數列
是遞增數列
C.數列![]() 的最大項是
的最大項是![]() D.數列
D.數列![]() 的最大項是
的最大項是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖![]() 所示,一條直角走廊寬為
所示,一條直角走廊寬為![]() ,
,![]()


(1)若位于水平地面上的一根鐵棒在此直角走廊內,且![]() ,試求鐵棒的長
,試求鐵棒的長![]() ;
;
(2)若一根鐵棒能水平地通過此直角走廊,求此鐵棒的最大長度;
(3)現有一輛轉動靈活的平板車,其平板面是矩形,它的寬![]() 為
為![]()
![]() 如圖2.平板車若想順利通過直角走廊,其長度
如圖2.平板車若想順利通過直角走廊,其長度![]() 不能超過多少米?
不能超過多少米?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(x+1)+![]() (a∈R).
(a∈R).
(1)當a=1時,求函數f(x)在點(0,f(0))處的切線方程;
(2)討論函數f(x)的極值;
(3)求證:ln(n+1)> ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}是等差數列,a1=f(x+1),a2=0,a3=f(x-1),其中f(x)=x2-4x+2.
(1)求通項公式an;
(2)若數列{an}為遞增數列,令bn=an+1+an+2+an+3+an+4,求數列{![]() }的前n項和Sn.
}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,橢圓
兩點,橢圓![]() 的右頂點為
的右頂點為![]() ,且滿足
,且滿足![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 、
、![]() ,且定點
,且定點![]() 滿足
滿足![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐![]() 的底面
的底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 為正三角形.
為正三角形.
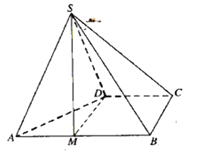
(1)點![]() 為棱
為棱![]() 上一點,若
上一點,若![]() 平面
平面![]() ,
,![]() ,求實數
,求實數![]() 的值;
的值;
(2)求點B到平面SAD的距離.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)由![]() 平面
平面![]() ,可證
,可證![]() ,進而證得四邊形
,進而證得四邊形![]() 為平行四邊形,根據
為平行四邊形,根據![]() ,可得
,可得![]() ;
;
(2)利用等體積法![]() 可求點
可求點![]() 到平面
到平面![]() 的距離.
的距離.
試題解析:((1)因為![]() 平面SDM,
平面SDM,
![]()
![]() 平面ABCD,
平面ABCD,
平面SDM ![]() 平面ABCD=DM,
平面ABCD=DM,
所以![]() ,
,
因為![]() ,所以四邊形BCDM為平行四邊形,又
,所以四邊形BCDM為平行四邊形,又![]() ,所以M為AB的中點.
,所以M為AB的中點.
因為![]() ,
,
![]() .
.

(2)因為![]()
![]() ,
, ![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
又因為![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
在平面![]() 內過點
內過點![]() 作
作![]() 直線
直線![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,
中,
因為![]() ,所以
,所以![]() ,
,
又由題知![]() ,
,
所以![]() ,
,
由已知求得![]() ,所以
,所以![]() ,
,
連接BD,則![]() ,
,
又求得![]() 的面積為
的面積為![]() ,
,
所以由![]() 點B 到平面
點B 到平面![]() 的距離為
的距離為![]() .
.
【題型】解答題
【結束】
19
【題目】小明在石家莊市某物流派送公司找到了一份派送員的工作,該公司給出了兩種日薪薪酬方案.甲方案:底薪100元,每派送一單獎勵1元;乙方案:底薪140元,每日前55單沒有獎勵,超過55單的部分每單獎勵12元.
(1)請分別求出甲、乙兩種薪酬方案中日薪![]() (單位:元)與送貨單數
(單位:元)與送貨單數![]() 的函數關系式;
的函數關系式;
(2)根據該公司所有派送員100天的派送記錄,發現派送員的日平均派送單數與天數滿足以下表格:
日均派送單數 | 52 | 54 | 56 | 58 | 60 |
頻數(天) | 20 | 30 | 20 | 20 | 10 |
回答下列問題:
①根據以上數據,設每名派送員的日薪為![]() (單位:元),試分別求出這100天中甲、乙兩種方案的日薪
(單位:元),試分別求出這100天中甲、乙兩種方案的日薪![]() 平均數及方差;
平均數及方差;
②結合①中的數據,根據統計學的思想,幫助小明分析,他選擇哪種薪酬方案比較合適,并說明你的理由.
(參考數據: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汕尾市基礎教育處為調查在校中學生每天放學后的自學時間情況,在本市的所有中學生中隨機抽取了120名學生進行調查,現將日均自學時間小于1小時的學生稱為“自學不足”者![]() 根據調查結果統計后,得到如下
根據調查結果統計后,得到如下![]() 列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為
列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為![]() .
.
非自學不足 | 自學不足 | 合計 | |
配有智能手機 | 30 | ||
沒有智能手機 | 10 | ||
合計 |
![]() 請完成上面的列聯表;
請完成上面的列聯表;
![]() 根據列聯表的數據,能否有
根據列聯表的數據,能否有![]() 的把握認為“自學不足”與“配有智能手機”有關?
的把握認為“自學不足”與“配有智能手機”有關?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,曲線
,曲線![]() 在
在![]() 處的切線經過點
處的切線經過點![]() .
.
(1)證明: ![]() ;
;
(2)若當![]() 時,
時, 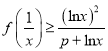 ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析;(2) ![]() .
.
【解析】試題分析:(1)先根據導數幾何意義得切線斜率為![]() ,再根據切線過點
,再根據切線過點![]() ,解得
,解得![]() 導數可得導函數零點,列表分析導函數符號變號規律可得函數單調性,根據函數單調性可得函數最小值為0,即得結論,(2)先化簡不等式為
導數可得導函數零點,列表分析導函數符號變號規律可得函數單調性,根據函數單調性可得函數最小值為0,即得結論,(2)先化簡不等式為![]() ,分離得
,分離得![]() ,再利用導數求函數
,再利用導數求函數![]() 單調性,利用羅伯特法則求最大值,即得
單調性,利用羅伯特法則求最大值,即得![]() 的取值范圍.
的取值范圍.
試題解析:(1)曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,即
,即![]()
由題意得![]() ,解得
,解得![]()
所以![]()
從而![]()
因為當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() .
.
所以![]() 在區間
在區間![]() 上是減函數,區間
上是減函數,區間![]() 上是增函數,
上是增函數,
從而![]() .
.
(2)由題意知,當![]() 時,
時, ![]() ,所以
,所以![]()
從而當![]() 時,
時, ![]() ,
,
由題意知 ,即
,即![]() ,其中
,其中![]()
設![]() ,其中
,其中![]()
設![]() ,即
,即![]() ,其中
,其中![]()
則![]() ,其中
,其中![]()
(1)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,所以
,所以![]() 是增函數
是增函數
從而當![]() 時,
時, ![]() ,
,
所以![]() 是增函數,從而
是增函數,從而![]() .
.
故當![]() 時符合題意.
時符合題意.
(2)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,
,
所以![]() 在區間
在區間![]() 上是減函數
上是減函數
從而當![]() 時,
時, ![]()
所以![]() 在
在![]() 上是減函數,從而
上是減函數,從而![]()
故當![]() 時不符合題意.
時不符合題意.
(3)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,所以
,所以![]() 是減函數
是減函數
從而當![]() 時,
時, ![]()
所以![]() 是減函數,從而
是減函數,從而![]()
故當![]() 時不符合題意
時不符合題意
綜上![]() 的取值范圍是
的取值范圍是![]() .
.
【題型】解答題
【結束】
22
【題目】在直角坐標坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() :
: ![]() .以
.以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸,與直角坐標系
軸的非負半軸為極軸,與直角坐標系![]() 取相同的長度單位,建立極坐標系.
取相同的長度單位,建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() (
(![]() )與曲線
)與曲線![]() 的異于極點的交點為
的異于極點的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com