
橢圓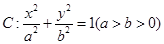 的左、右焦點分別為
的左、右焦點分別為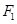 、
、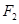 ,若橢圓
,若橢圓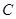 上恰好有6個不同的點
上恰好有6個不同的點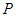 ,使得
,使得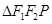 為等腰三角形,則橢圓
為等腰三角形,則橢圓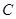 的離心率的取值范圍是( )
的離心率的取值范圍是( )
A.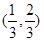 B.
B.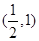 C.
C.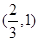 D.
D.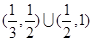
D
【解析】
試題分析:解:
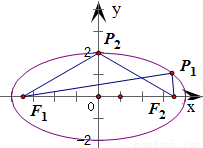
①當點P與短軸的頂點重合時,△F1F2P構成以F1F2為底邊的等腰三角形,此種情況有2個滿足條件的等腰△F1F2P;②當△F1F2P構成以F1F2為一腰的等腰三角形時,以F2P作為等腰三角形的底邊為例,∵F1F2=F1P,∴點P在以F1為圓心,半徑為焦距2c的圓上,因此,當以F1為圓心,半徑為2c的圓與橢圓C有2交點時,存在2個滿足條件的等腰△F1F2P,此時a-c<2c,解得a<3c,所以離心率e>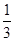 當e=
當e=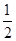 時,△F1F2P是等邊三角形,與①中的三角形重復,故e≠
時,△F1F2P是等邊三角形,與①中的三角形重復,故e≠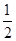 同理,當F1P為等腰三角形的底邊時,在e>
同理,當F1P為等腰三角形的底邊時,在e>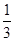 且e≠
且e≠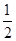 時也存在2個滿足條件的等腰△F1F2P,這樣,總共有6個不同的點P使得△F1F2P為等腰三角形,綜上所述,離心率的取值范圍是:e∈
時也存在2個滿足條件的等腰△F1F2P,這樣,總共有6個不同的點P使得△F1F2P為等腰三角形,綜上所述,離心率的取值范圍是:e∈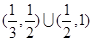 ,故選D.
,故選D.
考點:橢圓的標準方程和簡單幾何性質
點評:本題給出橢圓的焦點三角形中,共有6個不同點P使得△F1F2P為等腰三角形,求橢圓離心率e的取值范圍.著重考查了橢圓的標準方程和簡單幾何性質等知識,屬于基礎題


科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| PA |
| PB |
| AB |
| AP |
| PB |
| AB |
| PA |
| AB |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| PA |
| PB |
查看答案和解析>>
科目:高中數學 來源:2014屆黑龍江省高二上學期期末理科數學試卷(解析版) 題型:解答題
(本題12分)已知橢圓 的左、右焦點分別為F1、F2,其中F2也是拋物線
的左、右焦點分別為F1、F2,其中F2也是拋物線 的焦點,M是C1與C2在第一象限的交點,且
的焦點,M是C1與C2在第一象限的交點,且
(I)求橢圓C1的方程; (II)已知菱形ABCD的頂點A、C在橢圓C1上,頂點B、D在直線 上,求直線AC的方程。
上,求直線AC的方程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com