
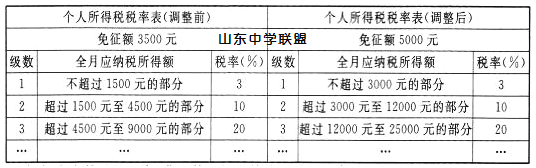
【題目】隨著經濟的發展,個人收入的提高.自2018年10月1日起,個人所得稅起征點和稅率的調整.調整如下:納稅人的工資、薪金所得,以每月全部收入額減除5000元后的余額為應納稅所得額.依照個人所得稅稅率表,調整前后的計算方法如下表:
(1)假如小李某月的工資、薪金等所得稅前收入總和不高于8000元,記![]() 表示總收入,y表示應納的稅,試寫出調整前后y關于
表示總收入,y表示應納的稅,試寫出調整前后y關于![]() 的函數表達式;
的函數表達式;
(2)某稅務部門在小李所在公司利用分層抽樣方法抽取某月100個不同層次員工的稅前收入,并制成下面的頻數分布表:
![]()
先從收入在[3000,5000)及[5000,7000)的人群中按分層抽樣抽取7人,再從中選4人作為新納稅法知識宣講員,求兩個宣講員不全是同一收入人群的概率;
(3)小李該月的工資、薪金等稅前收入為7500元時,請你幫小李算一下調整后小李的實際收入比調整前增加了多少?
【答案】(1)見解析;(2)![]() ;(3)見解析
;(3)見解析
【解析】
(1)依照個人所得稅稅率表,調整前后的計算方法得到調整前后y關于![]() 的函數表達式;
的函數表達式;
(2)利用分層抽樣明確各層所占人數,利用古典概型公式計算即可;
(3)按調整前起征點應納個稅為295元,調整后起征點應納個稅為75元,從而作出判斷.
(1)調整前y關于x的表達式為
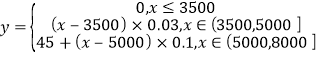 .
.
調整后y關于x的表達式為
![]() ,
,
(2)由頻數分布表可知從[3000,5000)及[5000,7000)的人群中按分層抽樣抽取7人,其中[3000,5000)中占3人,分別記為A,B,C,[5000,7000)中占4人,分別記為1,2,3,4,再從這7人中選2人的所有組合有:AB,AC,A1,A2,A3,A4,BC,B1,B2,B3,B4,C1,C2,C3,C4,12,13,14,23,24,34,共21種情況,
其中不在同一收入人群的有:Al,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,共12種,所以所求概率為![]() .
.
(3)由于小李的工資、薪金等收入為7500元,
按調整前起征點應納個稅為1500×3%+2500×10%=295元;
按調整后起征點應納個稅為2500×3%=75元,
比較兩個納稅方案可知,按調整后起征點應納個稅少交220元,
即個人的實際收入增加了220元,所以小李的實際收入增加了220元。


科目:高中數學 來源: 題型:
【題目】某校高一組織一次數學競賽,選取50名學生成績(百分制,均為整數),根據這50名學生的成績,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]()
![]()
![]()
![]()
![]()
![]() .
.
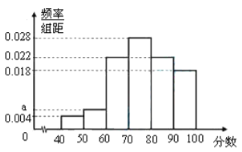
(1)求頻率分布直方圖中a的值;
(2)估計選取的50名學生在這次數學競賽中的平均成績;
(3)用分層抽樣的方法在分數段為![]() 的學生成績中抽取一個樣本容量為5的樣本,
的學生成績中抽取一個樣本容量為5的樣本,
再隨機抽取2人的成績,求恰有一人成績在分數段![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快遞公司收取快遞費用的標準是:重量不超過![]() 的包裹收費10元;重量超過
的包裹收費10元;重量超過![]() 的包裹,除收費10元之外,超過
的包裹,除收費10元之外,超過![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
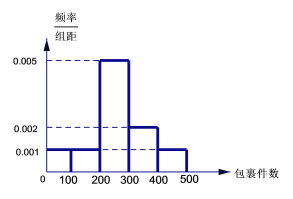
(1)求這60天每天包裹數量的平均值和中位數;
(2)該公司從收取的每件快遞的費用中抽取5元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.已知公司前臺有工作人員3人,每人每天工資100元,以樣本估計總體,試估計該公司每天的利潤有多少元?
(3)小明打算將![]() 四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過
四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過![]() ,求他支付的快遞費為45元的概率.
,求他支付的快遞費為45元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩隊參加聽歌猜歌名游戲,每隊![]() 人.隨機播放一首歌曲, 參賽者開始搶答,每人只有一次搶答機會,答對者為本隊贏得一分,答錯得零分, 假設甲隊中每人答對的概率均為
人.隨機播放一首歌曲, 參賽者開始搶答,每人只有一次搶答機會,答對者為本隊贏得一分,答錯得零分, 假設甲隊中每人答對的概率均為![]() ,乙隊中
,乙隊中![]() 人答對的概率分別為
人答對的概率分別為![]() ,且各人回答正確與否相互之間沒有影響.
,且各人回答正確與否相互之間沒有影響.
(1)若比賽前隨機從兩隊的![]() 個選手中抽取兩名選手進行示范,求抽到的兩名選手在同一個隊的概率;
個選手中抽取兩名選手進行示范,求抽到的兩名選手在同一個隊的概率;
(2)用![]() 表示甲隊的總得分,求隨機變量
表示甲隊的總得分,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(3)求兩隊得分之和大于4的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點F(1,0),定直線![]() ,動點M到點F的距離與到直線l的距離相等.
,動點M到點F的距離與到直線l的距離相等.
(1)求動點M的軌跡方程;
(2)設點![]() ,過點F作一條斜率大于0的直線交軌跡M于A,B兩點,分別連接PA,PB,若直線PA與直線PB不關于x軸對稱,求實數t的取值范圍.
,過點F作一條斜率大于0的直線交軌跡M于A,B兩點,分別連接PA,PB,若直線PA與直線PB不關于x軸對稱,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
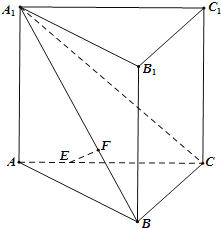
【題目】如圖,在直三棱柱![]() 側棱和底面垂直的棱柱
側棱和底面垂直的棱柱![]() 中,平面
中,平面![]() 側面
側面![]() ,
,![]() ,線段AC、
,線段AC、![]() 上分別有一點E、F且滿足
上分別有一點E、F且滿足![]() ,
,![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 求點E到直線
求點E到直線![]() 的距離;
的距離;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為支援邊遠地區教育事業的發展,現有5名師范大學畢業生主動要求赴西部某地區三所不同的學校去支教,每個學校至少去1人,甲、乙不能安排在同一所學校,則不同的安排方法有( )
A.180種B.150種C.90種D.114種
查看答案和解析>>
科目:高中數學 來源: 題型:
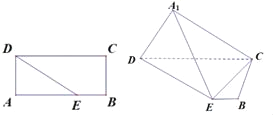
【題目】如圖(1)在矩形ABCD中,AB=5,AD=2,點E在線段AB上,且BE=1,將△ADE沿DE折起到△A1DE的位置,使得平面A1DE⊥平面BCDE,如圖(2).
(1)求證:CE⊥平面A1DE;
(2)求證:A1D⊥A1C;
(3)線段A1C上是否存在一點F,使得BF∥平面A1DE?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com