
【題目】已知函數![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線;
處的切線;
(2)若函數![]() 在其定義域內為增函數,求正實數
在其定義域內為增函數,求正實數![]() 的取值范圍;
的取值范圍;
(3)設函數![]() ,若在
,若在![]() 上至少存在一點
上至少存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1) 當![]() 時,
時,![]() ,求導,由
,求導,由![]() 求出切線斜率及點
求出切線斜率及點![]() ,即可求出切線方程;(2)由
,即可求出切線方程;(2)由![]() 在定義域區間
在定義域區間![]() 上恒成立得
上恒成立得![]() ,利用基本不等式求出函數
,利用基本不等式求出函數![]() 的最大值,即可求出
的最大值,即可求出![]() 的取值范圍;(3)構造函數
的取值范圍;(3)構造函數![]() ,由在區間
,由在區間![]() 上,函數
上,函數![]() 至少存在一點
至少存在一點![]() 使
使![]() ,即由在區間
,即由在區間![]() 上
上![]() ,求出
,求出![]() 的范圍即可.
的范圍即可.
試題解析:已知函數![]() .
.
(1)![]() ,
,![]() ,
,
![]() ,
,![]() , 故切線方程為:
, 故切線方程為:![]() .
.
(2)![]() ,由
,由![]() 在定義域
在定義域![]() 內為增函數,所以
內為增函數,所以![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 即
即![]() ,對
,對![]() 恒成立,設
恒成立,設![]() ,
,![]() ,
,
易知,![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,則
上單調遞減,則![]() ,
,
∴![]() ,即
,即![]() .
.
(3)設函數![]() ,
,![]() ,
,
則原問題![]() 在
在![]() 上至少存在一點
上至少存在一點![]() ,使得
,使得![]()
![]() ,
,
![]() 當
當![]() 時,
時,![]() ,則
,則![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,舍;
,舍;
![]() 當
當![]() 時,
時,![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,則
,則![]() ,舍;
,舍;![]() 當
當![]() 時,
時,![]() ,
,
則![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,整理得
,整理得![]() ,
,
綜上,![]() .
.


科目:高中數學 來源: 題型:
【題目】中國“一帶一路”戰略構思提出后, 某科技企業為抓住“一帶一路”帶來的機遇, 決定開發生產一款大型電子設備, 生產這種設備的年固定成本為![]() 萬元, 每生產
萬元, 每生產![]() 臺,需另投入成本
臺,需另投入成本![]() (萬元), 當年產量不足
(萬元), 當年產量不足![]() 臺時,
臺時,![]() (萬元); 當年產量不小于
(萬元); 當年產量不小于![]() 臺時
臺時![]() (萬元), 若每臺設備售價為
(萬元), 若每臺設備售價為![]() 萬元, 通過市場分析,該企業生產的電子設備能全部售完.
萬元, 通過市場分析,該企業生產的電子設備能全部售完.
(1)求年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (臺)的函數關系式;
(臺)的函數關系式;
(2)年產量為多少臺時 ,該企業在這一電子設備的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用紅、黃、藍三種不同顏色給圖中3個矩形隨機涂色,每個矩形只涂一種顏色,求: 
(1)3個矩形顏色都相同的概率;
(2)3個矩形顏色都不同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某次乒乓球比賽的決賽在甲乙兩名選手之間舉行,比賽采用五局三勝制,按以往比賽經驗,甲勝乙的概率為![]() .
.
(Ⅰ)求比賽三局甲獲勝的概率;
(Ⅱ)求甲獲勝的概率;
(Ⅲ)設甲比賽的次數為![]() ,求
,求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
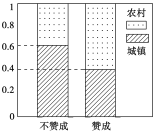
【題目】某省高考改革實施方案指出:該省高考考生總成績將由語文、數學、外語3門統一高考成績和學生自主選擇的學業水平等級性考試科目共同構成,該省教育廳為了解正在讀高中的學生家長對高考改革方案所持的贊成態度,隨機從中抽取了100名城鄉家長作為樣本進行調查,調查結果顯示樣本中有25人持不贊成意見,如圖是根據樣本的調查結果繪制的等高條形圖.
(1)根據已知條件與等高條形圖完成下面的![]() 列聯表,并判斷我們能否有95%的把握認為“贊成高考改革方案與城鄉戶口有關”?
列聯表,并判斷我們能否有95%的把握認為“贊成高考改革方案與城鄉戶口有關”?

注:![]() ,其中
,其中![]() .
.

(2)用樣本的頻率估計概率,若隨機在全省不贊成高考改革的家長中抽取3個,記這3個家長中是城鎮戶口的人數為![]() ,試求
,試求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題:
①經過定點P0(x0 , y0)的直線都可以用方程y﹣y0=k(x﹣x0)表示;
②經過定點A(0,b)的直線都可以用方程y=kx+b表示;
③不經過原點的直線都可以用方程 ![]() +
+ ![]() =1表示;
=1表示;
④經過任意兩個不同的 點P1(x1 , y1)、P2(x2 , y2)的直線都可以用方程(y﹣y1)(x2﹣x1)=(x﹣x1)(y2﹣y1)表示;
其中真命題的個數為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com