
【題目】為了解甲、乙兩奶粉廠的產品質量,采用分層抽樣的方法從甲、乙兩奶粉廠生產的產品中分別抽取16件和5件,測量產品中微量元素![]() 的含量(單位:毫克).下表是乙廠的5件產品的測量數據:
的含量(單位:毫克).下表是乙廠的5件產品的測量數據:
編號 | 1 | 2 | 3 | 4 | 5 |
| 170 | 178 | 166 | 176 | 180 |
| 74 | 80 | 77 | 76 | 81 |
(1)已知甲廠生產的產品共有96件,求乙廠生產的產品數量;
(2)當產品中的微量元素![]() 滿足
滿足![]() 且
且![]() 時,該產品為優等品.用上述樣本數據估計乙廠生產的優等品的數量;
時,該產品為優等品.用上述樣本數據估計乙廠生產的優等品的數量;
(3)從乙廠抽出的上述5件產品中,隨機抽取2件,求抽取的2件產品中優等品數![]() 的分布列及其均值(即數學期望).
的分布列及其均值(即數學期望).
【答案】(1)30;(2)18;(3)分布列見解析,期望為![]() .
.
【解析】分析:(1)設乙廠生產的產品數量為![]() 件,由
件,由![]() ,即可求得乙廠生產的產品數量;
,即可求得乙廠生產的產品數量;
(2)由題意,從乙廠抽取的![]() 件產品中,編號為
件產品中,編號為![]() 的產品是優等品,即
的產品是優等品,即![]() 件產品中有
件產品中有![]() 件是優等品,由此可估算出乙廠生產的優等品的數量;
件是優等品,由此可估算出乙廠生產的優等品的數量;
(3)![]() 可能的取值為
可能的取值為![]() ,求得取每個隨機變量時的概率,得到分布列,利用公式求解數學期望.
,求得取每個隨機變量時的概率,得到分布列,利用公式求解數學期望.
詳解:(1)設乙廠生產的產品數量為![]() 件,則
件,則![]() ,解得
,解得![]()
所以乙廠生產的產品數量為30件……………………3分
(2)從乙廠抽取的5件產品中,編號為2、5的產品是優等品,即5件產品中有3件是優等品
由此可以估算出乙廠生產的優等品的數量為![]() (件)………………6分
(件)………………6分
(3)![]() 可能的取值為0,1,2
可能的取值為0,1,2
![]()
∴![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 |
|
|
|
|
……………………10分
∴![]() ……………………12分
……………………12分


 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】某校為選拔參加“央視猜燈謎大賽”的隊員,在校內組織猜燈謎競賽.規定:第一階段知識測試成績不小于160分的學生進入第二階段比賽.現有200名學生參加知識測試,并將所有測試成績繪制成如下所示的頻率分布直方圖.
(Ⅰ)估算這200名學生測試成績的中位數,并求進入第二階段比賽的學生人數;
(Ⅱ)將進入第二階段的學生分成若干隊進行比賽.現甲、乙兩隊在比賽中均已獲得120分,進入最后搶答階段.搶答規則:搶到的隊每次需猜3條謎語,猜對1條得20分,猜錯1條扣20分.根據經驗,甲隊猜對每條謎語的概率均為 ![]() ,乙隊猜對前兩條的概率均為
,乙隊猜對前兩條的概率均為 ![]() ,猜對第3條的概率為
,猜對第3條的概率為 ![]() .若這兩隊搶到答題的機會均等,您做為場外觀眾想支持這兩隊中的優勝隊,會把支持票投給哪隊?
.若這兩隊搶到答題的機會均等,您做為場外觀眾想支持這兩隊中的優勝隊,會把支持票投給哪隊?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司開設的某險種的基本保費為![]() 萬元,今年參加該保險的人來年繼續購買該險種的投保人稱為續保人,續保人的下一年度的保費與其與本年度的出險次數的關聯如下:
萬元,今年參加該保險的人來年繼續購買該險種的投保人稱為續保人,續保人的下一年度的保費與其與本年度的出險次數的關聯如下:
本年度出險次數 |
|
|
|
|
|
|
下一次保費(單位:萬元) |
|
|
|
|
|
|
設今年初次參保該險種的某人準備來年繼續參保該險種,且該參保人一年內出險次數的概率分布列如下:
一年內出險次數 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
(![]() )求此續保人來年的保費高于基本保費的概率.
)求此續保人來年的保費高于基本保費的概率.
(![]() )若現如此續保人來年的保費高于基本保費,求其保費比基本保費高出
)若現如此續保人來年的保費高于基本保費,求其保費比基本保費高出![]() 的概率.
的概率.
(![]() )求該續保人來年的平均保費與基本保費的比值.
)求該續保人來年的平均保費與基本保費的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年春季,世界各地相繼出現流感疫情,這已經成為全球性的公共衛生問題.為了考察某種流感疫苗的效果,某實驗室隨機抽取100只健康小鼠進行試驗,得到如下列聯表:
感染 | 未感染 | 總計 | |
注射 | 10 | 40 | 50 |
未注射 | 20 | 30 | 50 |
總計 | 30 | 70 | 100 |
參照附表,在犯錯誤的概率最多不超過__________的前提下,可認為“注射疫苗”與“感染流感”有關系.
(參考公式:![]() .)
.)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4﹣4:極坐標與參數方程
極坐標系與直角坐標系xOy有相同的長度單位,以原點O為極點,以x軸正半軸為極軸.已知曲線C1的極坐標方程為 ![]() ,曲線C2的極坐標方程為ρsinθ=a(a>0),射線
,曲線C2的極坐標方程為ρsinθ=a(a>0),射線 ![]() ,
, ![]() 與曲線C1分別交異于極點O的四點A,B,C,D.
與曲線C1分別交異于極點O的四點A,B,C,D.
(Ⅰ)若曲線C1關于曲線C2對稱,求a的值,并把曲線C1和C2化成直角坐標方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知海島![]() 在海島
在海島![]() 北偏東
北偏東![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物體甲從海島
海里,物體甲從海島![]() 以
以![]() 海里/小時的速度沿直線向海島
海里/小時的速度沿直線向海島![]() 移動,同時物體乙從海島
移動,同時物體乙從海島![]() 沿著海島
沿著海島![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小時的速度移動.
海里/小時的速度移動.
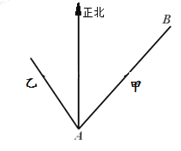
(1)問經過多長時間,物體甲在物體乙的正東方向;
(2)求甲從海島![]() 到達海島
到達海島![]() 的過程中,甲、乙兩物體的最短距離.
的過程中,甲、乙兩物體的最短距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在極坐標系(與平面直角坐標系
為參數).在極坐標系(與平面直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸)中,直線
軸非負半軸為極軸)中,直線![]() 的方程為
的方程為![]() .
.
(Ⅰ)求圓![]() 的普通方程及直線
的普通方程及直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設平面直角坐標系![]() 中的點
中的點![]() ,經過點
,經過點![]() 傾斜角為
傾斜角為![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com