
已知函數 (
( 為自然對數的底數)
為自然對數的底數)
(Ⅰ)若曲線 在點
在點 處的切線平行于
處的切線平行于 軸,求
軸,求 的值;
的值;
(Ⅱ)求函數 的極值;
的極值;
(Ⅲ)當 時,若直線
時,若直線 與曲線
與曲線 沒有公共點,求
沒有公共點,求 的最大值.
的最大值.
(Ⅰ) (Ⅱ)當
(Ⅱ)當 時,函數
時,函數 無極小值;
無極小值;
當 ,
, 在
在 處取得極小值
處取得極小值 ,無極大值(Ⅲ)
,無極大值(Ⅲ) 的最大值為
的最大值為
【解析】(Ⅰ)由 ,得
,得 .
.
又曲線 在點
在點 處的切線平行于
處的切線平行于 軸,
軸,
得 ,即
,即 ,解得
,解得 .
.
(Ⅱ) ,
,
①當 時,
時, ,
, 為
為 上的增函數,所以函數
上的增函數,所以函數 無極值.
無極值.
②當 時,令
時,令 ,得
,得 ,
, .
.
 ,
, ;
; ,
, .
.
所以 在
在 上單調遞減,在
上單調遞減,在 上單調遞增,
上單調遞增,
故 在
在 處取得極小值,且極小值為
處取得極小值,且極小值為 ,無極大值.
,無極大值.
綜上,當 時,函數
時,函數 無極小值;
無極小值;
當 ,
, 在
在 處取得極小值
處取得極小值 ,無極大值.
,無極大值.
(Ⅲ)當 時,
時,
令 ,
,
則直線 :
: 與曲線
與曲線 沒有公共點,
沒有公共點,
等價于方程 在
在 上沒有實數解.
上沒有實數解.
假設 ,此時
,此時 ,
, ,
,
又函數 的圖象連續不斷,由零點存在定理,可知
的圖象連續不斷,由零點存在定理,可知 在
在 上至少有一解,與“方程
上至少有一解,與“方程 在
在 上沒有實數解”矛盾,故
上沒有實數解”矛盾,故 .
.
又 時,
時, ,知方程
,知方程 在
在 上沒有實數解.
上沒有實數解.
所以 的最大值為
的最大值為 .
.
解法二:
(Ⅰ)(Ⅱ)同解法一.
(Ⅲ)當 時,
時, .
.
直線 :
: 與曲線
與曲線 沒有公共點,
沒有公共點,
等價于關于 的方程
的方程 在
在 上沒有實數解,即關于
上沒有實數解,即關于 的方程:
的方程:
 (*)
(*)
在 上沒有實數解.
上沒有實數解.
①當 時,方程(*)可化為
時,方程(*)可化為 ,在
,在 上沒有實數解.
上沒有實數解.
②當 時,方程(*)化為
時,方程(*)化為 .
.
令 ,則有
,則有 .
.
令 ,得
,得 ,
,
當 變化時,
變化時, 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
當 時,
時, ,同時當
,同時當 趨于
趨于 時,
時, 趨于
趨于 ,
,
從而 的取值范圍為
的取值范圍為 .
.
所以當 時,方程(*)無實數解,
時,方程(*)無實數解,
解得 的取值范圍是
的取值范圍是 .
.
綜上,得 的最大值為
的最大值為 .
.
此題的一二問考查的是最基本的函數切線問題及對極值含參情況的討論,所以導數公式必需牢記,對于參數的討論找到一個合理的分類標準做到不重不漏即可,可這往往又是學生最容易出現問題的地方.而第三問對于曲線是否無交點要懂得轉化成函數零點或方程根的個數問題處理,這也是常規處理含參就比較麻煩,平時要多加練習.
【考點定位】 本小題主要考查函數與導數,兩數的單調性、極值、零點等基礎知識,考查推理論證能力、運算求解 能力,考查函數與方程思想、數形結合思想、分類與整合思想、化歸與轉化思想.屬綜合要求比較高的難題.


科目:高中數學 來源: 題型:
(本小題共12分)已知函數![]() (
(![]() 為自然對數的底數),
為自然對數的底數),![]() (
(![]() 為常數),
為常數),![]() 是實數集
是實數集![]() 上的奇函數.(Ⅰ)求證:
上的奇函數.(Ⅰ)求證:![]() ;
;
(Ⅱ)討論關于![]() 的方程:
的方程:![]()
![]() 的根的個數;
的根的個數;
(Ⅲ)設![]() ,證明:
,證明:![]() (
(![]() 為自然對數的底數).
為自然對數的底數).
查看答案和解析>>
科目:高中數學 來源:2013-2014學年吉林通化第一中學高三上學期第二次月考理科數學試卷(解析版) 題型:解答題
已知函數 其中
其中 為自然對數的底數,
為自然對數的底數,  .
.
(1)設 ,求函數
,求函數 的最值;
的最值;
(2)若對于任意的 ,都有
,都有 成立,求
成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013屆浙江省溫州市高二下學期期中考試文科數學(解析版) 題型:解答題
已知函數 .(
.( 為自然對數的底)
為自然對數的底)
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)是否存在常數 使得
使得 對于任意的正數
對于任意的正數 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2012屆河北省高三第一學期期中考試文科數學試卷(解析版) 題型:解答題
已知.函數 .e為自然對數的底
.e為自然對數的底
(1)當 時取得最小值,求
時取得最小值,求 的值;
的值;
(2)令 ,求函數
,求函數 在點P
在點P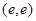 處的切線方程
處的切線方程
查看答案和解析>>
科目:高中數學 來源:2011-2012學年天津市高三第二次月考理科數學 題型:解答題
已知函數 其中
其中 為自然對數的底數
為自然對數的底數
(1)當 時,求曲線
時,求曲線 在
在 處的切線方程;
處的切線方程;
(2)若函數 為單調函數,求實數
為單調函數,求實數 的取值范圍;
的取值范圍;
(3)若 時,求函數
時,求函數 的極小值。
的極小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com